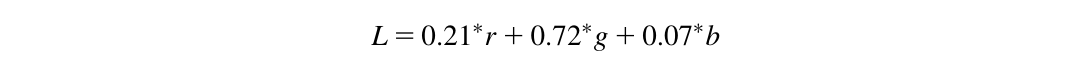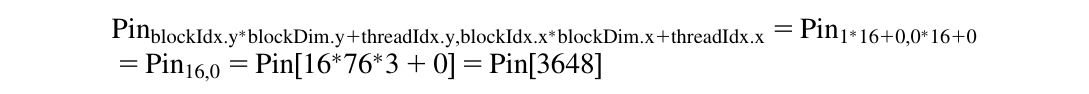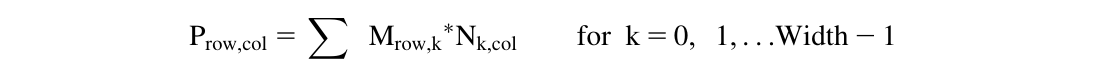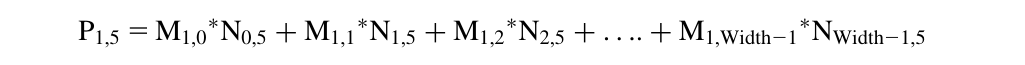第三章：多维网格和数据

在第2章《异构数据并行计算》中，我们学习了如何编写一个简单的CUDA C 程序，通过调用内核函数启动一个一维线程网格，以处理一维数组的元素。内核指定了由网格中的每个个体线程执行的语句。在本章中，我们将更一般地了解线程的组织方式，以及如何使用线程和块来处理多维数组。本章将使用多个示例，包括将彩色图像转换为灰度图像、对图像进行模糊处理和矩阵乘法。这些示例还有助于使读者熟悉在我们继续讨论GPU架构、内存组织和性能优化的未来章节之前，对数据并行性进行推理。

3.1 多维网格组织

在CUDA中，网格中的所有线程都执行相同的内核函数，并且它们依赖于坐标，即线程索引，以相互区分并识别要处理的数据的适当部分。正如我们在第2章《异构数据并行计算》中看到的那样，这些线程被组织成两级层次结构：一个网格由一个或多个块组成，每个块由一个或多个线程组成。块中的所有线程共享相同的块索引，可以通过 blockIdx（内置）变量访问。每个线程还有一个线程索引，可以通过 threadIdx（内置）变量访问。当一个线程执行内核函数时，对 blockIdx 和 threadIdx 变量的引用返回线程的坐标。在内核调用语句中，执行配置参数指定了网格的维度和每个块的维度。这些维度通过 gridDim 和 blockDim（内置）变量可用。

通常，一个网格是一个三维（3D）的块数组，每个块是一个三维（3D）的线程数组。在调用内核时，程序需要指定每个维度中网格和块的大小。这是通过内核调用语句的执行配置参数（在 <<<…>>>中）指定的。第一个执行配置参数指定了网格在块数上的维度。第二个指定了每个块在线程数上的维度。每个这样的参数都具有 dim3 类型，这是一个三个元素 x、y 和 z 的整数向量类型。这三个元素指定了三个维度的大小。程序员可以通过将未使用的维度的大小设置为1来使用少于三个维度。

例如，以下主机代码可用于调用 vecAddkernel() 内核函数，并生成一个由32个块组成的一维网格，每个块由128个线程组成。网格中线程的总数为 128 × 32 = 4096：

请注意，dimBlock 和 dimGrid 是由程序员定义的主机代码变量。只要它们具有 dim3 类型，它们就可以具有任何合法的 C 变量名。例如，以下语句实现了与上述语句相同的结果：

网格和块的维度也可以从其他变量计算。例如，图2.12中的内核调用可以写成如下形式：

这允许块的数量随着向量的大小而变化，以确保网格有足够的线程覆盖所有向量元素。在这个例子中，程序员选择将块大小固定为256。在内核调用时，变量 n 的值将确定网格的维度。如果 n 等于1000，网格将由四个块组成。如果 n 等于4000，网格将有16个块。在每种情况下，将有足够的线程覆盖所有的向量元素。一旦启动了网格，网格和块的维度将保持不变，直到整个网格执行完毕。

为了方便起见，CUDA 提供了一种特殊的快捷方式，用于调用具有一维（1D）网格和块的内核。可以使用算术表达式而不是 dim3 变量来指定 1D 网格和块的配置。在这种情况下，CUDA 编译器简单地将算术表达式视为 x 维度，并假定 y 和 z 维度为 1。这给我们提供了图2.12中显示的内核调用语句：

熟悉 C++ 的读者会意识到，这种用于 1D 配置的“简写”方便的实现是通过 C++ 构造函数和默认参数的工作方式来实现的。dim3 构造函数的参数的默认值为 1。当在期望 dim3 的地方传递一个单一值时，该值将传递给构造函数的第一个参数，而第二个和第三个参数将采用默认值 1。结果是一个 1D 网格或块，其中 x 维度的大小是传递的值，y 和 z 维度的大小为 1。

在内核函数中，gridDim 和 blockDim 变量的 x 字段根据执行配置参数的值进行了预初始化。例如，如果 n 等于 4000，在 vectAddKernel 内核中对 gridDim.x 和 blockDim.x 的引用将分别得到 16 和 256。请注意，在内核函数中，与主机代码中的 dim3 变量不同，这些变量的名称是 CUDA C 规范的一部分，不能更改。也就是说，gridDim 和 blockDim 是内核中的内置变量，并始终反映网格和块的维度。

在 CUDA C 中，gridDim.x 允许的值范围从 1 到 $2^{31}-1$(设备的计算能力低于 3.0 的允许 blockIdx.x 的值在 1 到 $2^{16}-1$ 之间 )，gridDim.y 和 gridDim.z 的值范围从 1 到 $2^{16}-1$（65,535）。同一块中的所有线程共享相同的 blockIdx.x、blockIdx.y 和 blockIdx.z 值。在块之间，blockIdx.x 的值范围从 0 到 gridDim.x-1，blockIdx.y 的值范围从 0 到 gridDim.y-1，blockIdx.z 的值范围从 0 到 gridDim.z-1。

现在，我们关注块的配置。每个块都组织成一个 3D 线程数组。通过将 blockDim.z 设置为 1，可以创建二维（2D）块。通过将 blockDim.y 和 blockDim.z 都设置为 1，可以创建一维块，就像 vectorAddKernel 的示例中那样。如前所述，网格中的所有块都具有相同的维度和大小。块的每个维度中的线程数由内核调用时的第二个执行配置参数指定。在内核中，可以通过 blockDim 的 x、y 和 z 字段访问此配置参数。

在当前的 CUDA 系统中，块的总大小限制为 1024 个线程。这些线程可以以任何方式分布在三个维度上，只要总线程数不超过 1024。例如，(512, 1, 1)、(8, 16, 4) 和 (32, 16, 2) 这样的 blockDim 值都是允许的，但 (32, 32, 2) 不允许，因为总线程数将超过 1024。

图3.1 CUDA 网格组织的多维示例。

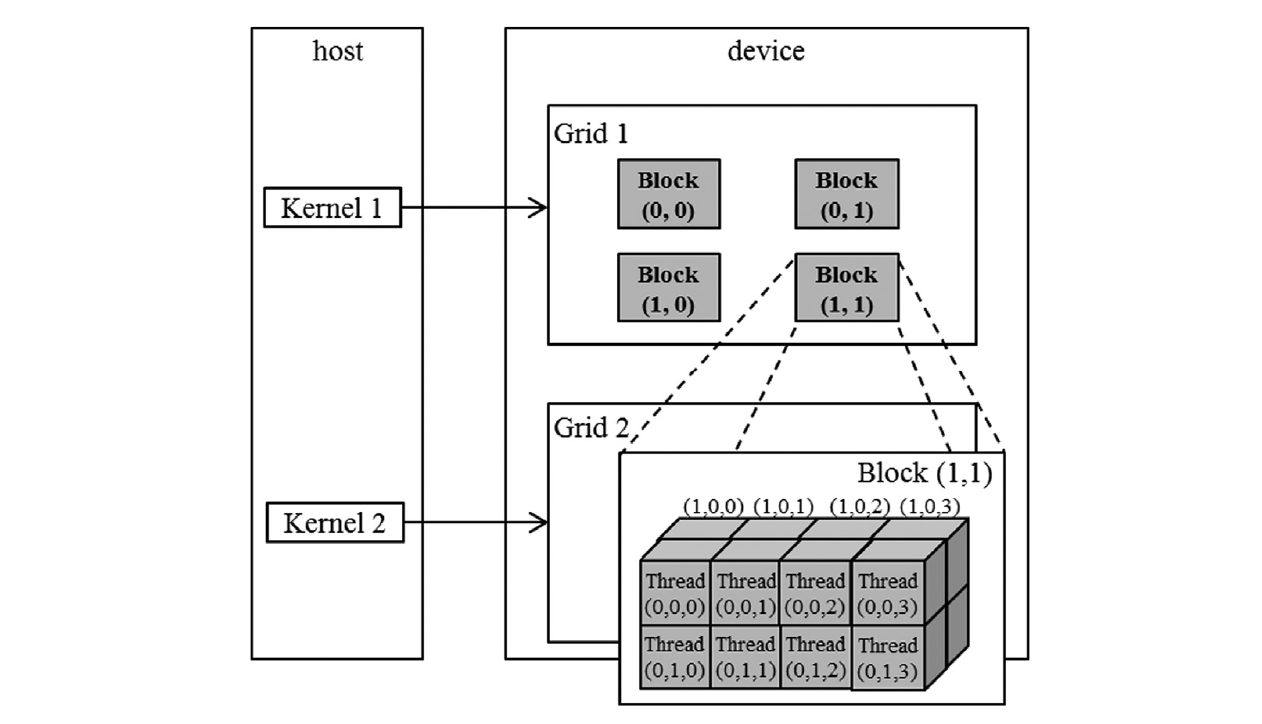
网格及其块不需要具有相同的维度。网格的维度可以高于其块，反之亦然。例如，图 3.1 展示了一个带有 gridDim 为 (2, 2, 1) 和 blockDim 为 (4, 2, 2) 的小型示例网格。可以使用以下主机代码创建这样的网格：

图 3.1 中的网格由四个块组成，排列成一个 2x3x2 的数组。每个块都标有 (blockIdx.y, blockIdx.x)。例如，块 (1,0) 具有 blockIdx.y 为 1 和 blockIdx.x 为 0。请注意，块和线程标签的排序是最高维度先出现的。此表示法使用的排序与用于设置配置参数的 C 语句中的排序相反，其中最低维度首先出现。在标记块时采用的这种反向排序在说明线程坐标映射到访问多维数据的数据索引时更为合适。

每个 threadIdx 也由三个字段组成：x 坐标 threadIdx.x，y 坐标 threadIdx.y 和 z 坐标 threadIdx.z。图 3.1 说明了块内线程的组织。在这个例子中，每个块被组织成一个 4x3x2 的线程数组。由于网格中的所有块都具有相同的维度，我们只展示其中一个。图 3.1 将块 (1,1) 展开，显示其 16 个线程。例如，线程 (1,0,2) 具有 threadIdx.z 为 1，threadIdx.y 为 0，以及 threadIdx.x 为 2。请注意，在这个例子中，我们有 4 个包含 16 个线程的块，总共有 64 个线程在网格中。我们使用这些较小的数字是为了使图示简单化。典型的 CUDA 网格包含数千到数百万个线程。

图 3.2 使用二维线程网格处理一张尺寸为 62x76 的图片 P。

3.2 将线程映射到多维数据

1D、2D或3D线程组织的选择通常基于数据的性质。例如，图像是像素的二维数组。使用由2D块组成的2D网格通常方便处理图像中的像素。图3.2展示了这样一种安排，用于处理一张大小为62x76的图片P（垂直或y方向有62个像素，水平或x方向有76个像素）【我们将按降序引用多维数据的维度：先是 z 维度，然后是 y 维度，依此类推。例如，对于垂直或 y 维度有 n 个像素，水平或 x 维度有 m 个像素的图片，我们将其称为 n x m 图片。这遵循了 C 语言多维数组索引的约定。例如，在文本和图中，为了简洁起见，我们可以将 P[y][x] 称为 $P_{y,x}$。不幸的是，这种顺序与在 gridDim 和 blockDim 维度中排列数据维度的顺序相反。当我们基于将由其线程处理的多维数组定义线程网格的维度时，这种差异可能会特别令人困惑。】。假设我们决定使用一个16x16的块，其中x方向有16个线程，y方向也有16个线程。在y方向需要四个块，在x方向需要五个块，这导致了4x5=20个块，如图3.2所示。粗线标记了块的边界。阴影区域描述了覆盖像素的线程。每个线程被分配处理一个像素，其y和x坐标由其blockIdx、blockDim和threadIdx变量的值派生：

垂直（行）坐标：row = blockIdx.y * blockDim.y + threadIdx.y 水平（列）坐标：coordinate = blockIdx.x * blockDim.x + threadIdx.x

例如，要由块（1,0）的线程（0,0）处理的像素元素Pin，可以如下识别：

请注意，在图3.2中，y方向多了两个额外的线程，x方向多了四个额外的线程。也就是说，我们将生成64x80=5120个线程来处理62x76的像素。这类似于图2.9中使用四个256线程块处理1000元素向量的1D核心vecAddKernel的情况。回想一下，图2.10中的if语句是为了防止额外的24个线程产生作用。同样，我们应该期望图像处理核函数会使用if语句来测试线程的垂直和水平索引是否落在有效的像素范围内。

我们假设主机代码使用整数变量n来跟踪y方向的像素数，另一个整数变量m来跟踪x方向的像素数。我们进一步假设输入图片数据已经被复制到设备全局内存，并且可以通过指针变量Pin_d访问。输出图片已经在设备内存中分配，并且可以通过指针变量Pout_d访问。以下主机代码可用于调用一个2D核心colorToGrayscaleConversion来处理图片，如下所示：

在这个例子中，为了简单起见，我们假设块的维度固定为16x16。另一方面，网格的维度取决于图片的维度。要处理一个1500x2000（300万像素）的图片，我们将生成11,750个块：在y方向上有94个块，在x方向上有125个块。在核心函数中，对于gridDim.x、gridDim.y、blockDim.x和blockDim.y的引用将分别得到125、94、16和16。

在展示核心代码之前，我们首先需要了解C语句如何访问动态分配的多维数组的元素。理想情况下，我们希望像访问Pin_d这样的2D数组，其中第j行和第i列的元素可以通过Pin_d[j][i]来访问。然而，CUDA C是在ANSI C标准的基础上开发的，该标准要求在编译时需要知道Pin的列数，才能将其作为2D数组进行访问。不幸的是，对于动态分配的数组，这些信息在编译时是未知的。事实上，使用动态分配的数组的部分原因之一是允许这些数组的大小和维度根据运行时的数据大小而变化。因此，动态分配的2D数组的列数信息在设计时并不是在编译时已知的。结果，程序员需要显式地将动态分配的2D数组“线性化”或“展平”成当前CUDA C中的等效1D数组。

实际上，C中的所有多维数组都是线性化的。这是由于现代计算机中使用了“平”内存空间（参见“内存空间”侧边栏）。对于静态分配的数组，编译器允许程序员使用更高维的索引语法，如Pin_d[j][i]，来访问它们的元素。在底层，编译器将它们线性化为等效的1D数组，并将多维索引语法转换为1D偏移。对于动态分配的数组，由于在编译时缺乏维度信息，当前的CUDA C编译器将这种转换的工作留给了程序员。

内存空间 内存空间是一个简化的视图，展示了处理器在现代计算机中如何访问内存。每个正在运行的应用程序通常与一个内存空间相关联。要由应用程序处理的数据以及为应用程序执行的指令存储在其内存空间中的位置。每个位置通常可以容纳一个字节，并具有一个地址。需要多个字节的变量（例如float为4字节，double为8字节）存储在连续的字节位置中。从内存空间中访问数据值时，处理器提供起始地址（起始字节位置的地址）和所需字节数。

大多数现代计算机至少具有4GB大小的位置，其中每个GB为1,073,741,824（$2^30$）。所有位置都带有从0到最大使用数字的地址。由于每个位置只有一个地址，我们说内存空间具有“平”组织。因此，所有多维数组最终都被“展平”为等效的一维数组。虽然C程序员可以使用多维数组语法访问多维数组的元素，但编译器将这些访问转换为指向数组起始元素的基指针，以及从这些多维索引计算出的一维偏移。

有至少两种将2D数组线性化的方式。一种方法是将同一行的所有元素放入连续的位置。然后，这些行依次放入内存空间。这种排列称为行主排列，如图3.3所示。为了提高可读性，我们使用Mj,i表示M中第j行和第i列的元素。Mj,i等效于C表达式M[j][i]，但稍微更易读。图3.3显示了一个例子，其中4x4矩阵M被线性化为一个包含16个元素的1D数组，首先是所有第0行的元素，然后是第1行的四个元素，依此类推。因此，M在第j行和第i列的元素的1D等效索引为j * 4 + i。j * 4跳过了第j行之前的所有行的元素。然后，i项选择了第j行的部分中的正确元素。例如，M2,1的1D索引为2 * 4 + 1 = 9。这在图3.3中有所说明，其中M9是M2,1的1D等效形式。这是C编译器线性化2D数组的方式。

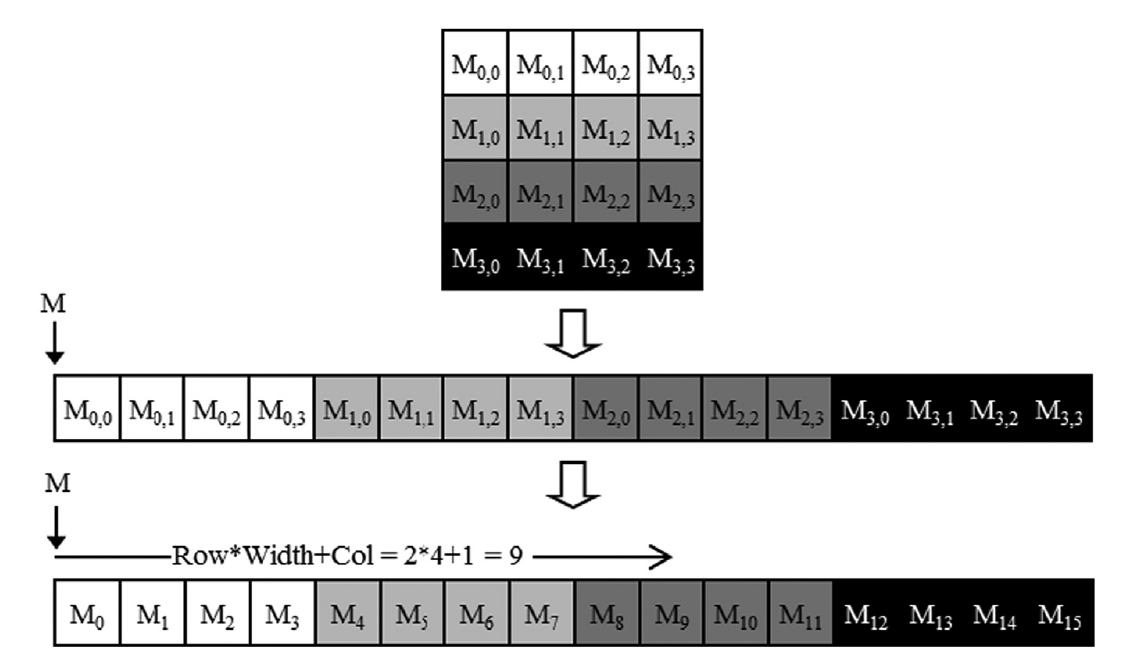图3.3 2D C数组的行主排列。结果是一个等效的1D数组，通过索引表达式j * Width + i访问，该表达式用于访问数组中第j行和第i列的元素，每行有Width个元素。

另一种线性化2D数组的方法是将同一列的所有元素放入连续的位置。然后，这些列依次放入内存空间。这种排列称为列主排列，被FORTRAN编译器使用。注意，2D数组的列主排列等效于其转置形式的行主排列。我们不会花更多时间在这上面，除了提到那些主要以前使用FORTRAN编程经验的读者应该知道，CUDA C使用行主排列而不是列主排列。此外，许多设计用于FORTRAN程序的C库使用列主排列以匹配FORTRAN编译器的排列。因此，这些库的手册通常告诉用户如果从C程序调用这些库，他们应该对输入数组进行转置。

图3.4 colorToGrayscaleConversion的源代码，具有2D线程映射到数据的功能。

我们现在准备学习colorToGrayscaleConversion的源代码，如图3.4所示。核心代码使用以下方程将每个彩色像素转换为其灰度对应物：

在水平方向上，总共有 blockDim.x * gridDim.x 个线程。类似于vecAddKernel示例，下面的表达式生成从0到 blockDim.x * gridDim.x - 1 的所有整数值（第6行）：

我们知道 gridDim.x * blockDim.x 大于或等于宽度（从主机代码传入的 m 值）。我们至少有和水平方向上的像素数量一样多的线程。我们还知道至少有和垂直方向上的像素数量一样多的线程。因此，只要我们测试并确保仅有行和列值都在范围内的线程，即（col < width）&&（row < height），我们就能够覆盖图片中的每个像素（第7行）。

由于每行有 width 个像素，我们可以生成位于行 row 和列 col 处的像素的1D索引，即 row * width + col（第10行）。这个1D索引 grayOffset 是 Pout 的像素索引，因为输出灰度图像中的每个像素都是1字节（unsigned char）。使用我们的 62x76 图像示例，由块（1,0）的线程（0,0）计算的 Pout 像素的线性化1D索引如下公式所示：

至于 Pin，我们需要将灰度像素索引乘以 3（即三个颜色通道，第13行），因为每个彩色像素都存储为三个元素（r、g、b），每个元素都是1字节。得到的 rgbOffset 给出了 Pin 数组中颜色像素的起始位置。我们从 Pin 数组的三个连续字节位置中读取 r、g 和 b 的值（第14行到第16行），进行灰度像素值的计算，并使用 grayOffset 将该值写入 Pout 数组（第19行）。在我们的 62x76 图像示例中，由块（1,0）的线程（0,0）处理的 Pin 像素的第一个分量的线性化1D索引可以用以下公式计算：

正在访问的数据是从字节偏移3648开始的3个字节。图3.5说明了在处理我们的62x76示例时colorToGrayscaleConversion的执行过程。假设使用16x16块调用colorToGrayscaleConversion核函数，将生成64x80个线程。网格将有4x5=20个块：垂直方向有4个块，水平方向有5个块。块的执行行为将落入图3.5中四个不同情况中的一个，分别显示为四个阴影区域。

图3.5中标为1的第一个区域包含属于覆盖图片大部分像素的12个块的线程。这些线程的col和row值都在范围内；所有这些线程都通过if语句测试，处理图片的深色阴影区域中的像素。也就是说，每个块中的所有16x16=256个线程都将处理像素。

图3.5中标为2的第二个区域包含属于覆盖图片右上角像素的中等阴影区域的三个块的线程。尽管这些线程的row值始终在范围内，但其中一些线程的col值超过了76的m值。这是因为水平方向上的线程数量始终是程序员选择的blockDim.x值（在这种情况下为16）的倍数。覆盖76像素所需的最小的16的倍数是80。因此，每行中的12个线程将发现其col值在范围内，并将处理像素。每行中的其余四个线程将发现其col值超出范围，因此将不满足if语句的条件。这些线程将不处理任何像素。总体而言，每个这些块中的16x16=256个线程中的12x16=192个线程将处理像素。

图3.5 使用16x16块覆盖的76x62图片。

图3.5中标为3的第三个区域包含覆盖图片中等阴影区域的四个左下角块的线程。尽管这些线程的col值始终在范围内，但其中一些线程的row值超过了62的n值。这是因为垂直方向上的线程数量始终是程序员选择的blockDim.y值（在这种情况下为16）的倍数。覆盖62像素所需的最小的16的倍数是64。因此，每列中的14个线程将发现其row值在范围内，并将处理像素。每列中的其余两个线程将不满足if语句的条件，将不处理任何像素。总体而言，256个线程中的16x14=224个线程将处理像素。

第四个区域，图3.5中标为4的区域，包含覆盖图片右下角浅阴影区域的线程。与区域2类似，每个顶部的14行中的4个线程将发现其col值超出范围。与区域3类似，该块的整个底部两行将发现其row值超出范围。总体而言，256个线程中的仅有16x12=168个线程将处理像素。

我们可以通过在线性化数组时加入另一个维度，轻松地将我们对2D数组的讨论扩展到3D数组。这是通过将数组的每个“平面”依次放入地址空间中完成的。假设程序员使用变量m和n分别跟踪3D数组的列数和行数。程序员还需要在调用内核时确定blockDim.z和gridDim.z的值。在内核中，数组索引将涉及另一个全局索引：

对3D数组P的线性化访问将采用P[plane * m * n + row * m + col]的形式。处理3D P数组的内核需要检查所有三个全局索引，即plane、row和col，是否都在数组的有效范围内。

在CUDA内核中使用3D数组的应用将在第8章“Stencil”中进一步研究。

3.3 图像模糊：一个更复杂的核

我们已经学习了vecAddKernel和colorToGrayscaleConversion这两个例子，其中每个线程仅对一个数组元素执行少量的算术操作。这些核函数很好地完成了它们的目的：演示基本的CUDA C程序结构和数据并行执行概念。此时，读者应该提出一个显而易见的问题：CUDA C程序中的所有线程是否都执行这种简单和琐碎的独立操作？答案是否定的。在真实的CUDA C程序中，线程经常对其数据执行复杂的操作，并需要相互协作。在接下来的几章中，我们将着手处理越来越复杂的例子，展示这些特点。我们将从一个图像模糊函数开始。

图3.6 原始图像（左）和模糊版本（右）

图像模糊可以平滑像素值的突变，同时保留对于识别图像关键特征至关重要的边缘。图3.6展示了图像模糊的效果。简单来说，我们使图像变得模糊。对于人眼来说，模糊的图像往往会掩盖细节，呈现出“整体印象”或图像中的主题对象。在计算机图像处理算法中，图像模糊的一个常见用例是通过使用周围清晰像素值来校正图像中有问题的像素值，从而减轻噪声和颗粒状渲染效果的影响。在计算机视觉中，图像模糊可以用于使边缘检测和对象识别算法专注于主题对象，而不被大量的细粒度对象拖慢。在显示中，有时通过模糊图像的其余部分来突出显示图像的特定部分。

在数学上，图像模糊函数计算输出图像像素值，作为围绕输入图像中的像素的一个像素块的加权总和。正如我们将在第7章“卷积”中学到的那样，这些加权总和的计算属于卷积模式。在本章中，我们将采用一种简化的方法，通过对围绕目标像素的N x N像素块进行简单平均值。为了保持算法简单，我们不会根据像素距离目标像素的距离对任何像素的值施加权重。在实践中，对像素值施加权重在卷积模糊方法中是相当常见的，例如高斯模糊。

图3.7 每个输出像素是输入图像中一片周围像素及其自身的平均值

图3.7显示了使用3x3x3像素块进行图像模糊的示例。当计算位于(row, col)位置的输出像素值时，我们看到像素块以位于(row, col)位置的输入像素为中心。3x3x3像素块跨足了三行（row-1, row, row+1）和三列（col-1, col, col+1）。例如，计算位于(25, 50)的输出像素的九个像素的坐标是(24, 49), (24, 50), (24, 51), (25, 49), (25, 50), (25, 51), (26, 49), (26, 50)和(26, 51)。

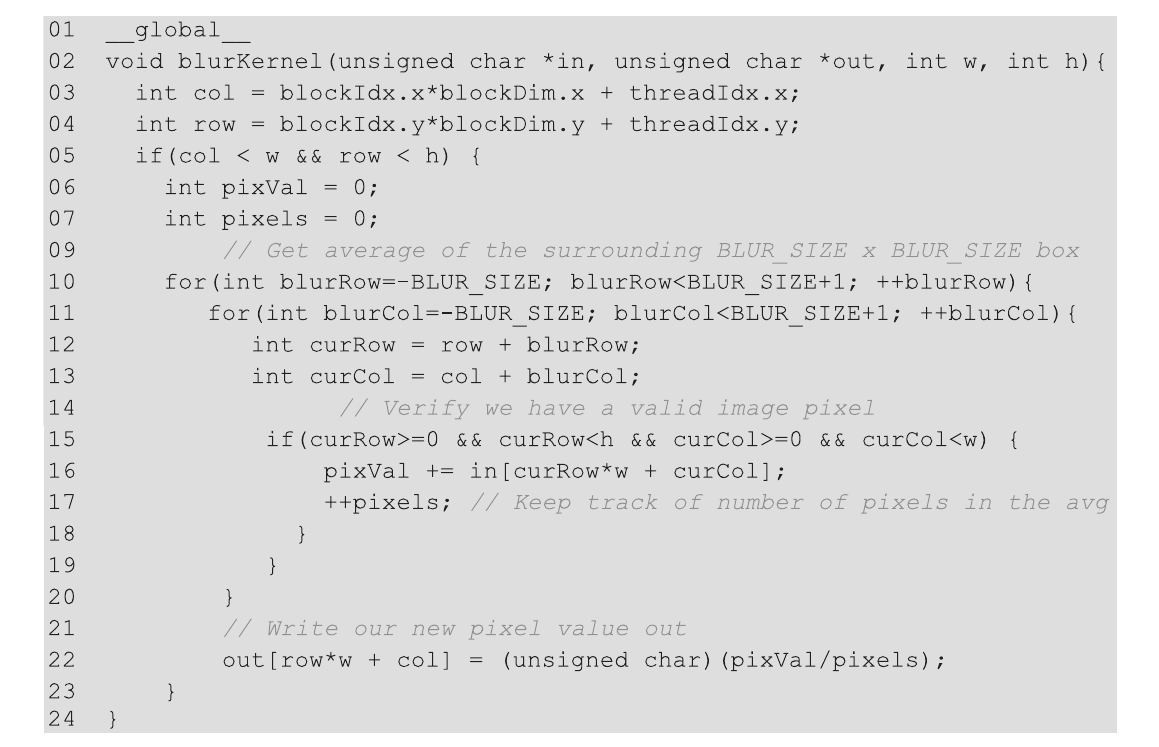图3.8 每个输出像素是输入图像中一片周围像素及其自身的平均值

图3.8显示了一个图像模糊的核函数。与colorToGrayscaleConversion中使用的策略类似，我们使用每个线程来计算一个输出像素。也就是说，线程到输出数据的映射保持不变。因此，在内核的开头，我们看到了计算col和row索引的熟悉过程（第03-04行）。我们还看到了熟悉的if语句，验证col和row是否根据图像的高度和宽度在有效范围内（第05行）。只有col和row索引都在值范围内的线程才被允许参与执行。

如图3.7所示，col和row的值还表示用于计算线程输出像素的输入像素块的中心像素位置。图3.8中的嵌套for循环（第10-11行）遍历了像素块中的所有像素。我们假设程序定义了一个常量BLUR_SIZE。BLUR_SIZE的值设置为使其成为像素块一侧（半径）上的像素数量，而2*BLUR_SIZE+1则给出了像素块一个维度上的总像素数。例如，对于一个3x3x3的像素块，BLUR_SIZE设置为1，而对于一个7x7x7的像素块，BLUR_SIZE设置为3。外层循环遍历像素块的行。对于每一行，内层循环遍历像素块的列。

在我们的3x3x3像素块示例中，BLUR_SIZE为1。对于计算输出像素(25, 50)的线程，在外层循环的第一次迭代中，curRow变量为row-BLUR_SIZE，即(25-1) = 24。因此，在外层循环的第一次迭代中，内层循环遍历像素块中的第24行像素。内层循环使用curCol变量从col-BLUR_SIZE（即50-1=49）迭代到col+BLUR_SIZE（即51）。因此，在外层循环的第一次迭代中，处理的像素为(24, 49)、(24, 50)和(24, 51)。读者应该验证，在外层循环的第二次迭代中，内层循环遍历像素(25, 49)、(25, 50)和(25, 51)。最后，在外层循环的第三次迭代中，内层循环遍历像素(26, 49)、(26, 50)和(26, 51)。

图3.9 处理靠近图像边缘的像素的边界条件

第16行使用curRow和curCol的线性化索引访问当前迭代中访问的输入像素的值。它将像素值累加到一个运行总和变量pixVal中。第17行通过递增pixels变量记录已将一个更多的像素值添加到运行总和中。在处理完像素块中的所有像素之后，第22行通过将pixVal值除以pixels值计算像素块中像素的平均值。它使用row和col的线性化索引将结果写入其输出像素。

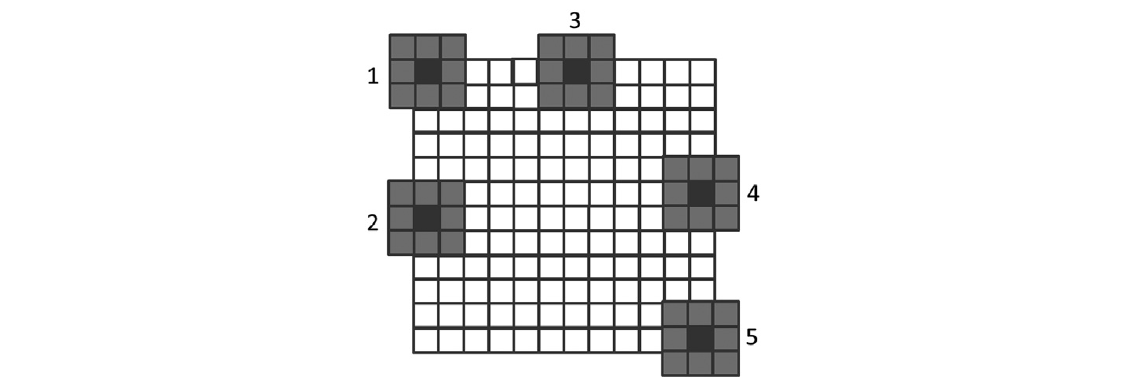
第15行包含一个条件语句，保护第16行和第17行的执行。例如，在计算图像边缘附近的输出像素时，像素块可能会超出输入图像的有效范围。这在假设3x3x3像素块的情况下在图3.9中进行了说明。在案例1中，正在模糊位于左上角的像素。预期像素块中的九个像素中的五个在输入图像中不存在。在这种情况下，输出像素的行和列值分别为0和0。在嵌套循环的执行过程中，九次迭代的curRow和curCol值分别是(21, 2 1)、(21,0)、(21,1)、(0, 2 1)、(0,0)、(0,1)、(1, 2 1)、(1,0)和(1,1)。请注意，对于在图像外部的五个像素，至少有一个值小于0。if语句的curRow < 0和curCol < 0条件捕获这些值并跳过第16行和第17行的执行。因此，只有四个有效像素的值被累加到运行总和变量中。pixels值也仅正确增加了四次，以便可以在第22行正确地计算平均值。

读者应该通过图3.9中的其他情况并分析blurKernel中嵌套循环的执行行为。请注意，大多数线程将在其分配的3x3x3像素块中找到所有像素。它们将累加所有九个像素。但是，对于四个角上的像素，负责的线程将只累加四个像素。对于四条边上的其他像素，负责的线程将累加六个像素。这些变化是需要使用变量pixels跟踪实际累积的像素数量的原因。

3.4 矩阵乘法

矩阵乘法，简称矩乘，是基本线性代数子程序标准的重要组成部分（参见“线性代数函数”侧边栏）。它是许多线性代数求解器的基础，如LU分解。对于使用卷积神经网络进行深度学习，矩阵乘法也是一个重要的计算，将在第16章“深度学习”中详细讨论。

线性代数函数

线性代数运算在科学和工程应用中被广泛使用。在基本线性代数子程序（BLAS）中，这是一个发布执行基本代数运算的库的事实标准，有三个级别的线性代数函数。随着级别的提高，函数执行的操作数量增加。级别1的函数执行形式为y = αx + y的向量运算，其中x和y是向量，α是标量。我们的向量加法示例是α=1的级别1函数的特例。级别2的函数执行形式为y = αAx + βy的矩阵-向量运算，其中A是矩阵，x和y是向量，α和β是标量。我们将在稀疏线性代数中研究级别2函数的一种形式。级别3的函数执行矩阵-矩阵运算形式为C = αAB + βC，其中A、B和C是矩阵，α和β是标量。我们的矩阵乘法示例是α=1且β=0的级别3函数的特例。这些BLAS函数很重要，因为它们被用作更高级别代数函数的基本构建块，如线性系统求解器和特征值分析。正如我们稍后将讨论的那样，BLAS函数的不同实现在顺序计算机和并行计算机中的性能差异可以达到数量级的差异。

矩阵M（i行j列）与矩阵N（j行k列）之间的矩阵乘法会产生一个矩阵P（i行k列）。在执行矩阵乘法时，输出矩阵P的每个元素都是矩阵M的一行与矩阵N的一列的内积。我们将继续使用约定，其中$P_{row, col}$是输出矩阵中在垂直方向的第row位置和水平方向的第col位置的元素。如图3.10所示，Prow,col（P中的小正方形）是由矩阵M的第row行（在M中显示为水平条带）和矩阵N的第col列（在N中显示为垂直条带）形成的向量的内积。两个向量的内积，有时称为点积，是两个向量元素的乘积之和。也就是说，

图3.10 通过矩阵P的切片块进行多块矩阵乘法。

例如，在图3.10中，假设row等于1，col等于5，

为了使用CUDA实现矩阵乘法，我们可以使用与我们用于colorToGrayscaleConversion相同的方法将网格中的线程映射到输出矩阵P的元素。也就是说，每个线程负责计算一个P元素。由每个线程计算的P元素的行和列索引与之前相同：

图3.11 使用一个线程计算一个P元素的矩阵乘法核心

通过这种一对一的映射，行和列线程索引也成为它们输出元素的行和列索引。图3.11显示了基于这种线程到数据映射的核心源代码。读者应该立即注意到计算行和列（第03-04行）的熟悉模式以及if语句测试行和列是否都在范围内（第05行）。这些语句几乎与colorToGrayscaleConversion中的相应语句相同。唯一的显著区别是我们做了一个简化假设，即matrixMulKernel只需处理方阵，因此我们用Width替换了宽度和高度。这种线程到数据的映射有效地将P分成了tile，其中一个tile在图3.10中显示为浅色正方形。每个块负责计算其中一个tile。

现在我们关注每个线程所做的工作。回想一下，$P_{row,col}$是由M的row行和N的col列的内积计算得到的。在图3.11中，我们使用一个for循环来执行这个内积运算。在进入循环之前，我们将本地变量Pvalue初始化为0（第06行）。循环的每次迭代从M的row行和N的col列中获取一个元素，将两个元素相乘，并将乘积累加到Pvalue中（第08行）。

首先让我们关注在for循环中访问M元素。M被线性化为等效的1D数组，使用行主序。也就是说，M的各行在内存空间中一个接一个地放置，从第0行开始。因此，第1行的起始元素是M[1 * Width]，因为我们需要考虑第0行的所有元素。通常，row行的起始元素是M[row * Width]。由于一行的所有元素都放置在连续的位置，row行的第k个元素位于M[row * Width + k]。这是图3.11（第08行）中使用的线性化数组偏移。

现在我们将注意力转向访问N。如图3.11所示，col列的起始元素是第0行的第col个元素，即N[col]。访问col列中的下一个元素需要跳过整行。这是因为同一列的下一个元素是下一行的相同元素。因此，col列的第k个元素是N[k * Width + col]（第08行）。

当执行退出for循环时，所有线程在Pvalue变量中有它们的P元素值。然后，每个线程使用1D等效的索引表达式row * Width + col来写入它的P元素（第10行）。再次说明，这种索引模式类似于colorToGrayscaleConversion核函数中使用的模式。

图3.12 matrixMulKernel执行的简单例子

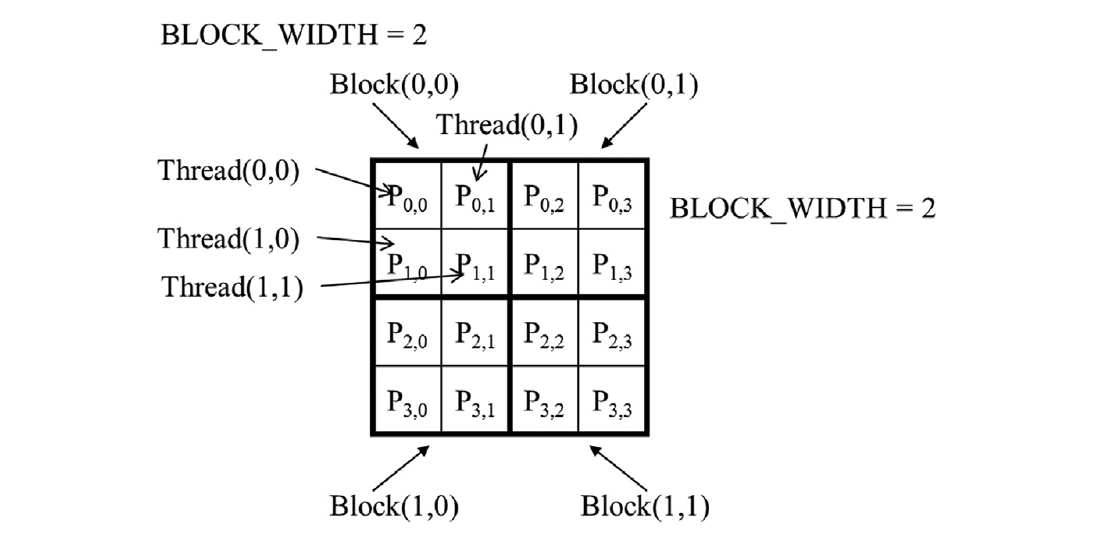
我们现在使用一个小例子来说明矩阵乘法核心的执行。图3.12显示了一个4x3的P矩阵，其中BLOCK_WIDTH为2。尽管这样小的矩阵和块大小并不现实，但它们允许我们将整个示例放入一张图片中。P矩阵被分为四个tile，每个块计算一个tile。我们通过创建2x2的线程数组的块来实现，每个线程计算一个P元素。在这个例子中，块（0,0）的线程（0,0）计算$P_{0,0}$，而块（1,0）的线程（0,0）计算$P_{2,0}$。

图3.13 一个线程块的矩阵乘法操作。

matrixMulKernel中的行和列索引标识线程要计算的P元素。行索引还标识M的行，列索引标识N的列作为线程的输入值。图3.13说明了每个线程块中的乘法操作。对于小矩阵乘法示例，块（0,0）中的线程产生四个点积。块（0,0）中线程（1,0）的行和列索引分别为0 * 0 + 1 = 1 和0 * 0 + 0 = 0。因此，该线程映射到$P_{1,0}$并计算M的第1行和N的第0列的点积。

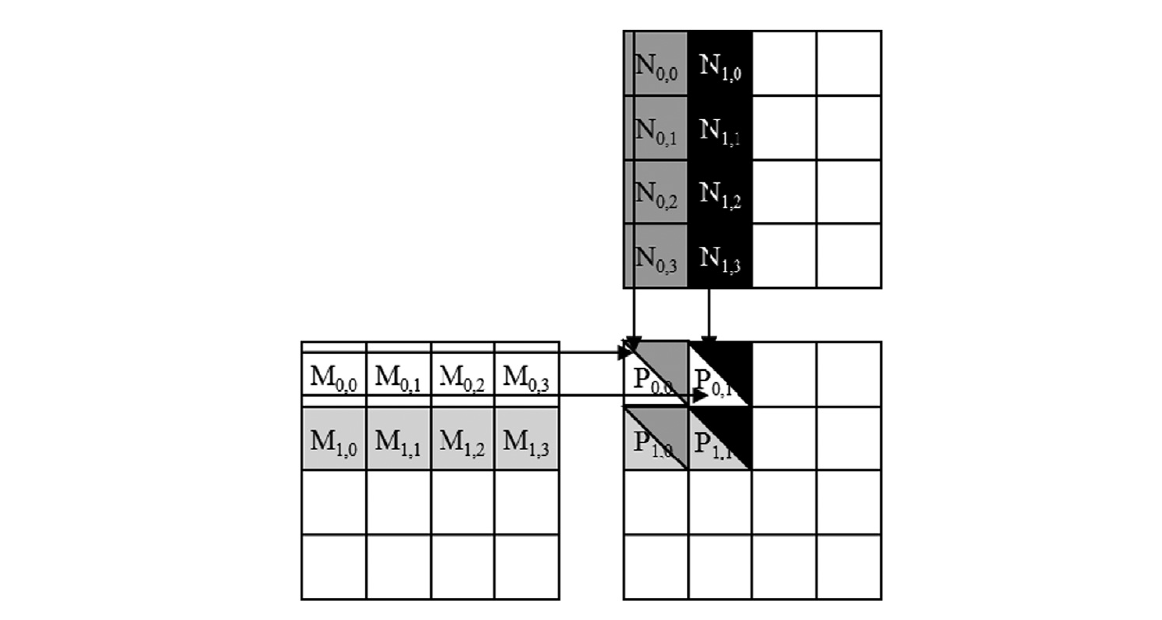
让我们走一遍在块（0,0）中的线程（0,0）中执行图3.11的for循环。在迭代0（k为0）期间，row * Width + k为0 * 4 + 0 * 1 = 0，k * Width + col为0 * 4 + 0 * 1 = 0。因此，访问的输入元素为M[0]和N[0]，它们分别是$M_{0,0}$和$N_{0,0}$的1D等效。注意这确实是M的第0行和N的第0列的第0个元素。在迭代1（k为1）期间，row * Width + k为0 * 4 + 1 * 1 = 1，k * Width + col为1 * 4 + 0 * 1 = 4。因此，我们访问M[1]和N[4]，它们分别是$M_{0,1}$和$N_{1,0}$的1D等效。这是M的第0行和N的第0列的第1个元素。在迭代2（k为2）期间，row * Width + k为0 * 4 + 2 * 1 = 2，k * Width + col为2 * 4 + 0 * 1 = 8，结果为M[2]和N[8]。因此，访问的元素是M0,2和N 2,0的1D等效。最后，在迭代3（k为3）期间，row * Width + k为0 * 4 + 3 * 1 = 3，k * Width + col为3 * 4 + 0 * 1 = 12，结果为M[3]和N[12]，即$M_{0,3}$和$N_{3,0}$的1D等效。我们现在已经验证了for循环对于块（0,0）中的线程（0,0）执行了M的第0行和N的第0列的内积。在循环结束后，线程写入了P[row * Width + col]，即P[0]。这是P 0,0的1D等效，因此块（0,0）中的线程（0,0）成功地计算了M的第0行和N的第0列的内积，并将结果存入$P_{0,0}$。

我们将其留作读者的练习，手动执行和验证块（0,0）中其他线程或其他块的for循环。

由于网格的大小受限于每个网格的最大块数和每个块的线程数，matrixMulKernel能处理的最大输出矩阵P的大小也受到这些约束的限制。在需要计算大于此限制的输出矩阵的情况下，可以将输出矩阵分成子矩阵，其大小可以由网格覆盖，并使用主机代码为每个子矩阵启动不同的网格。或者，我们可以更改核心代码，以便每个线程计算更多的P元素。我们将在本书的后面探讨这两个选项。

3.5 总结

CUDA的网格和块是多维的，最多可以有三个维度。网格和块的多维性对于组织线程以映射到多维数据是有用的。核心执行配置参数定义了网格及其块的维度。blockIdx和threadIdx中的唯一坐标允许网格的线程识别自己及其数据域。程序员有责任在核函数中使用这些变量，以便线程能够正确地识别要处理的数据部分。在访问多维数据时，程序员通常需要将多维索引线性化为1D偏移。原因是在C中动态分配的多维数组通常按行主序存储为1D数组。我们使用逐渐复杂的示例使读者熟悉使用多维网格处理多维数组的机制。这些技能将为理解并行模式及其相关的优化技术奠定基础。

• ← Previous Post
• Next Post →