第五章：内存架构和数据局部性

到目前为止，我们已经学习了如何编写一个CUDA核函数，并如何配置和协调其执行，以供大量线程使用。我们还研究了当前GPU硬件的计算架构以及如何在该硬件上调度线程执行。在本章中，我们将专注于GPU的片上内存架构，并开始研究如何组织和定位数据，以便大量线程高效访问。到目前为止，我们研究过的CUDA核函数可能只能实现底层硬件潜在速度的一小部分。这种性能不佳是因为全局内存通常使用芯片外DRAM实现，具有较长的访问延迟（数百个时钟周期）和有限的访问带宽。虽然理论上拥有许多可用于执行的线程可以容忍长时间的内存访问延迟，但很容易遇到这样的情况：全局内存访问路径中的交通拥堵阻止了除了极少数线程之外的所有线程都取得进展，从而使一些流多处理器（SMs）中的核心处于空闲状态。为了避免这种拥堵，GPU提供了许多额外的片上内存资源，用于访问数据，可以消除大部分与全局内存的通信。在本章中，我们将研究不同类型的内存用于提升CUDA核函数的执行性能。

5.1 内存访问效率的重要性

我们可以通过计算图3.11中最常执行的矩阵乘法核心代码的预期性能水平来说明内存访问效率的影响，该代码在图5.1中部分复制。就执行时间而言，核心的最重要部分是执行 M 行与 N 列的点积的 for 循环。

图5.1 矩阵乘法核心的最常执行部分。

在循环的每次迭代中，为了一个浮点乘法和一个浮点加法，会执行两次全局内存访问。全局内存访问会从 M 和 N 数组中获取元素。浮点乘法操作将这两个元素相乘，浮点加法操作将乘积累加到 Pvalue 中。因此，浮点操作（FLOP）与从全局内存访问的字节数（B）的比率为2 FLOP 对 8 B，即 0.25 FLOP/B。我们将这个比率称为计算与全局内存访问的比率，它定义为程序区域内每个字节访问的全局内存所执行的 FLOP 数。在文献中，这个比率有时也称为算术强度或计算强度。

计算与全局内存访问的比率对CUDA核函数的性能有重大影响。例如，Ampere A100 GPU 的峰值全局内存带宽为 1555 GB/秒。由于矩阵乘法核心执行的操作是 0.25 OP/B，因此全局内存带宽限制了内核可以执行的单精度FLOP的吞吐量，为每秒 389 giga FLOP（GFLOPS），通过将 1555 GB/秒与 0.25 FLOP/B 相乘获得。然而，389 GFLOPS仅占A100 GPU的峰值单精度操作吞吐量的2%，后者为 19,500 GFLOPS。A100还配备了称为张量核心的专用单元，用于加速矩阵乘法运算。如果考虑到A100的张量核心峰值单精度浮点吞吐量为156,000 GFLOPS，那么389 GFLOPS仅占峰值的0.25%。因此，矩阵乘法核心的执行受限于数据从内存传输到GPU核心的速率。我们将受内存带宽限制的程序的执行速度称为内存密集型(bound)程序。

屋顶线(Roofline)模型

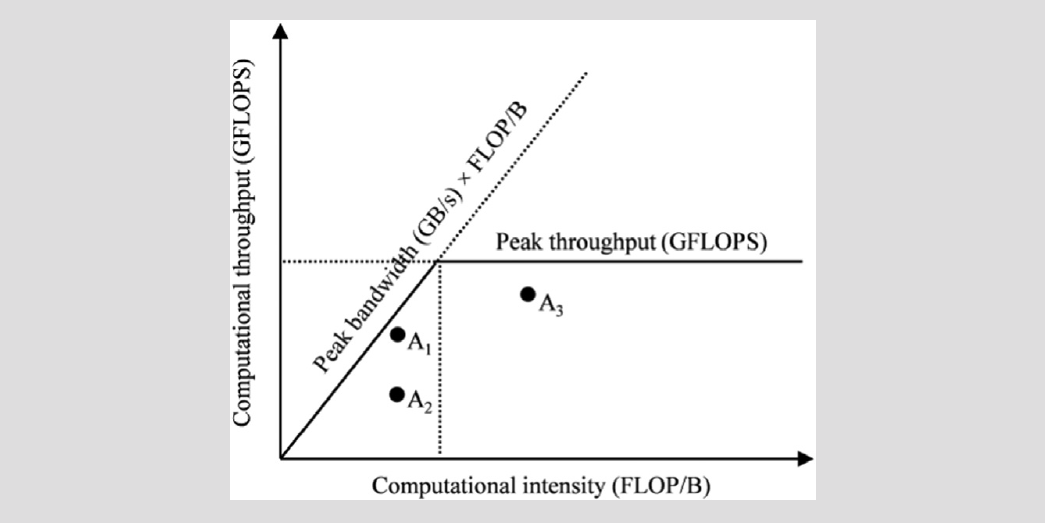
屋顶线模型是一种用于评估应用程序相对于其运行硬件极限所实现性能的视觉模型。下面是屋顶线模型的一个基本示例。

在x轴上，我们有以FLOP/B为单位的算术或计算强度。它反映了应用程序为每个加载的字节数据所执行的工作量。在y轴上，我们有以GFLOPS为单位的计算吞吐量。图中的两条线反映了硬件的限制。水平线由硬件可以维持的峰值计算吞吐量（GFLOPS）确定。从原点开始的带有正斜率的线由硬件可以维持的峰值内存带宽确定。图中的一个点代表了一个应用程序，其操作强度在x轴上，其在y轴上实现的计算吞吐量。当然，这些点将位于两条线的下方，因为它们不能实现比硬件峰值更高的吞吐量。

点相对于这两条线的位置告诉我们有关应用程序效率的信息。靠近这两条线的点表明应用程序有效地使用了内存带宽或计算单元，而远离这两条线的应用程序表示资源使用不足。这两条线的交点表示应用程序从内存密集型转换为计算密集型的计算强度值。计算强度较低的应用程序是内存密集型的，并且无法实现峰值吞吐量，因为它们受到内存带宽的限制。计算强度较高的应用程序是计算密集型的，并且不受内存带宽的限制。

举例来说，点 A1 和 A2 都代表内存密集型应用程序，而 A3 代表计算密集型应用程序。A1有效地利用资源，并且接近峰值内存带宽，而 A2 则没有。对于A2，可能有进一步优化的空间，以通过改善内存带宽利用率来提高吞吐量。然而，对于A1，提高吞吐量的唯一方法是增加应用程序的计算强度。

要提高此核心的性能，我们需要通过减少它执行的全局内存访问次数来提高核心的计算与全局内存访问比率。例如，为了充分利用A100 GPU提供的 19,500 GFLOPS，至少需要（19,500 GOP/秒）/（1555 GB/秒）=12.5 OP/B的比率。这个比率意味着，对于每个访问的 4 字节浮点值，必须执行大约 50 次浮点操作！这种比率能够达到的程度取决于正在进行的计算中固有的数据重用。我们建议读者阅读“屋顶线模型”旁注，以了解有关使用计算强度分析程序潜在性能的有用模型。

正如我们将看到的，矩阵乘法提供了减少全局内存访问的机会，这可以通过相对简单的技术来捕获。矩阵乘法函数的执行速度可以根据全局内存访问的减少程度而相差几个数量级。因此，矩阵乘法为这些技术提供了一个极好的初始示例。本章介绍了一种常用的减少全局内存访问次数的技术，并在矩阵乘法上演示了该技术。

5.2 CUDA内存类型

CUDA设备包含几种类型的内存，可以帮助程序员改善计算与全局内存访问的比率。图5.2显示了这些CUDA设备内存。在图的底部，我们看到全局内存和常量内存。这两种类型的内存都可以由主机进行写入（W）和读取（R）。全局内存也可以由设备进行写入和读取，而常量内存则支持设备进行短延迟、高带宽的只读访问。我们在第2章异构数据并行计算中介绍了全局内存，而在第7章卷积中将详细讨论常量内存。

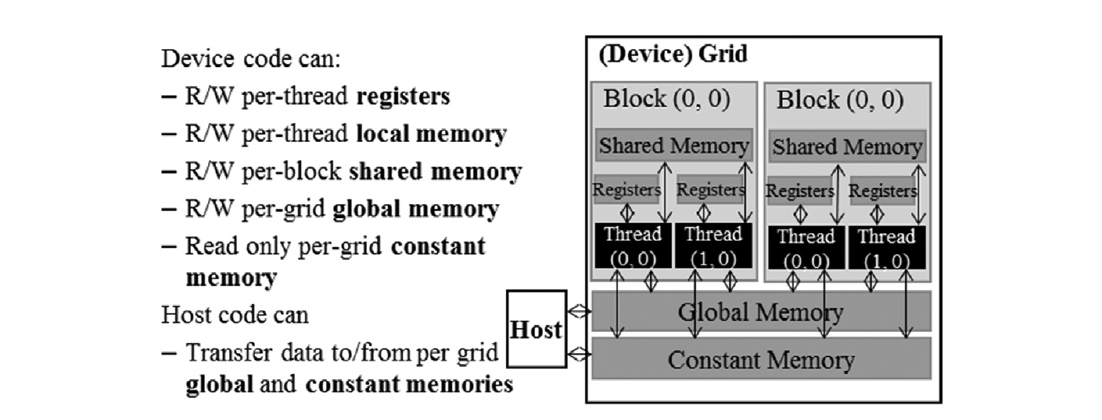图 5.2 CUDA设备内存模型的（不完整）概述。图中未显示的一个重要类型的CUDA内存是纹理内存，因为本教材未涵盖其使用。

另一种类型的内存是本地内存，它也可以被读取和写入。本地内存实际上位于全局内存中，并具有类似的访问延迟，但它不跨线程共享。每个线程都有自己的一部分全局内存，它将其用作自己的私有本地内存，其中放置了线程私有但无法在寄存器中分配的数据。这些数据包括静态分配的数组、溢出的寄存器和线程调用堆栈的其他元素。

图5.2中的寄存器和共享内存是芯片上的内存。驻留在这些类型的内存中的变量可以以非常高的速度以高度并行的方式访问。寄存器分配给各个线程；每个线程只能访问自己的寄存器。典型的内核函数通常使用寄存器来保存对每个线程私有的频繁访问的变量。共享内存分配给线程块；块中的所有线程都可以访问为该块声明的共享内存变量。共享内存是线程通过共享其输入数据和中间结果来合作的有效手段。通过在CUDA内存类型中声明CUDA变量，CUDA程序员决定了变量的可见性和访问速度。

CPU与GPU寄存器架构

CPU和GPU之间不同的设计目标导致了不同的寄存器架构。正如我们在第4章计算架构和调度中看到的那样，当CPU在不同线程之间进行上下文切换时，它将外出线程的寄存器保存到内存中，并从内存中恢复传入线程的寄存器。相比之下，GPU通过将所有计划在处理块上的线程的寄存器保留在处理块的寄存器文件中来实现零开销调度。这样，线程warp之间的切换是即时的，因为传入线程的寄存器已经在寄存器文件中。因此，GPU寄存器文件的大小需要比CPU寄存器文件大得多。

我们还在第4章计算架构和调度中看到，GPU支持动态资源分区，其中SM可以为每个线程提供少量的寄存器并执行大量的线程，或者为每个线程提供更多的寄存器并执行较少的线程。因此，GPU寄存器文件需要设计以支持寄存器的动态分区。相比之下，CPU寄存器架构为每个线程的寄存器分配了固定的寄存器集，而不考虑线程对寄存器的实际需求。

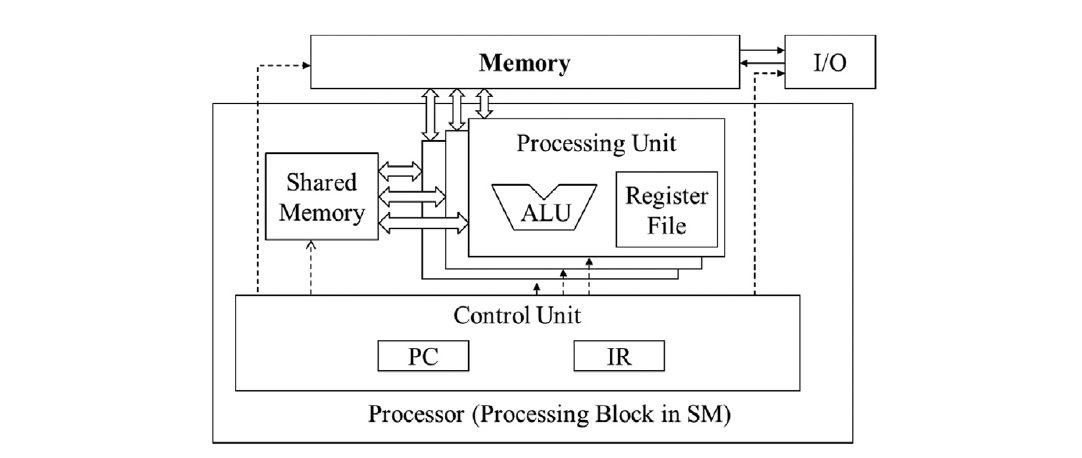
图 5.3 基于冯·诺依曼模型的现代计算机中的内存与寄存器。

要充分了解寄存器、共享内存和全局内存之间的差异，我们需要更详细地了解这些不同类型的内存如何在现代处理器中实现和使用。正如我们在第4章计算架构和调度的“Warp和SIMD硬件”中讨论的那样，几乎所有现代处理器都源自1945年约翰·冯·诺依曼提出的模型，如图5.3所示。CUDA设备也不例外。CUDA设备中的全局内存映射到图5.3中的内存框。处理器框对应于我们今天通常看到的处理器芯片边界。全局内存位于处理器芯片外部，并采用DRAM技术实现，这意味着访问延迟较长，访问带宽相对较低。寄存器对应于冯·诺依曼模型中的“寄存器文件”。寄存器文件位于处理器芯片上，这意味着访问延迟非常短，访问带宽与全局内存相比大大提高。在典型的设备中，所有SM上所有寄存器文件的聚合访问带宽至少比全局内存高两个数量级。此外，当变量存储在寄存器中时，其访问不再消耗芯片外全局内存带宽。这将反映为计算与全局内存访问比率的增加。

在现代计算机中，每次访问寄存器都比访问全局内存涉及的指令更少，这是一个微妙的点。在大多数现代处理器中，算术指令都具有“内置”寄存器操作数。例如，浮点加法指令可能具有以下形式：

fadd r1, r2, r3

其中r2和r3是指定寄存器文件中可以找到输入操作数值的位置的寄存器编号。存储浮点加法结果值的位置由r1指定。因此，当算术指令的操作数在寄存器中时，不需要额外的指令将操作数值提供给算术逻辑单元（ALU），即进行算术计算的地方。

与此同时，如果操作数值在全局内存中，处理器需要执行内存加载操作将操作数值提供给ALU。例如，如果浮点加法指令的第一个操作数在全局内存中，涉及的指令可能看起来像以下示例：

load r2, r4, offset
fadd r1, r2, r3

其中load指令将偏移值添加到r4的内容中以形成操作数值的地址。然后，它访问全局内存并将该值放入寄存器r2中。一旦操作数值在r2中，fadd指令就会使用r2和r3中的值执行浮点加法，并将结果放入r1中。由于处理器每个时钟周期只能获取和执行有限数量的指令，带有额外加载的版本可能比没有额外加载的版本需要更长时间来处理。这是将操作数放入寄存器可以提高执行速度的另一个原因。

最后，将操作数值放入寄存器更可取的另一个微妙原因。在现代计算机中，从寄存器文件访问值所消耗的能量至少比从全局内存访问值的能量低一个数量级。与从全局内存访问值相比，从寄存器访问值在能量效率方面具有巨大优势。我们很快将详细了解访问这两种硬件结构中的速度和能量差异。另一方面，正如我们很快将了解的那样，每个线程可用的寄存器数量在今天的GPU中是相当有限的。正如我们在第4章计算架构和调度中看到的那样，在全占用场景中，如果寄存器使用量超过限制，应用程序的占用率可能会降低。因此，我们也需要尽可能避免超额订阅这一有限资源。

图 5.4 CUDA设备SM中的共享内存与寄存器的对比。

图5.4显示了CUDA设备中的共享内存和寄存器。尽管两者都是芯片上的内存，但在功能和访问成本上有很大差异。共享内存设计为驻留在处理器芯片上的内存空间的一部分。当处理器访问驻留在共享内存中的数据时，它需要执行内存加载操作，就像访问全局内存中的数据一样。但是，由于共享内存位于芯片上，它的访问延迟和吞吐量比全局内存要低得多。由于需要执行加载操作，共享内存的延迟和带宽低于寄存器。在计算机体系结构术语中，共享内存是一种暂存器(scratchpad)内存形式。

CUDA中共享内存和寄存器之间的一个重要区别是，驻留在共享内存中的变量可以被块中的所有线程访问。这与寄存器数据相反，后者是线程私有的。也就是说，共享内存旨在支持块中的线程之间的高效、高带宽的数据共享。如图5.4所示，CUDA设备SM通常使用多个处理单元允许多个线程同时进行进度（请参阅第2章异构数据并行计算中的“线程”侧栏）。块中的线程可以分布在这些处理单元上。因此，这些CUDA设备中共享内存的硬件实现通常设计为允许多个处理单元同时访问其内容，以支持块中线程之间的高效数据共享。

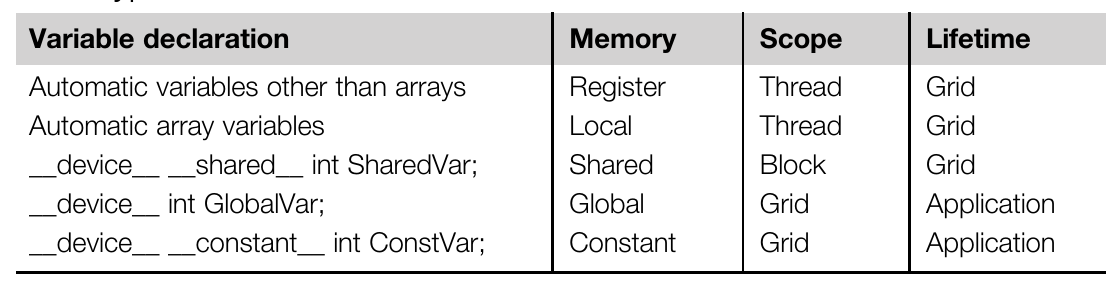
到目前为止，应该清楚寄存器、本地内存、共享内存和全局内存都具有不同的功能、延迟和带宽。因此，了解如何声明变量以使其驻留在所需类型的内存中非常重要。表5.1提供了将程序变量声明为各种内存类型的CUDA语法。每个这样的声明还为其声明的CUDA变量指定了作用域和生命周期。作用域标识了可以访问变量的线程集：单个线程、块中的所有线程或所有网格的所有线程。如果变量的作用域是单个线程，则为每个线程创建变量的私有版本；每个线程只能访问其私有版本的变量。例如，如果一个内核声明的变量的作用域是一个线程，并且启动了一百万个线程，将创建一百万个版本的变量，以便每个线程初始化和使用其自己的变量版本。

表5.1 CUDA变量声明类型修饰符及每种类型的特性。

生命周期告诉我们程序执行期间变量可供使用的部分：可以是在网格执行期间，也可以是整个应用程序期间。如果变量的生命周期在网格执行期间，它必须在内核函数体内声明，并且只能由内核代码使用。如果内核被多次调用，则该变量的值不会在这些调用之间保持。每次调用都必须初始化变量才能使用。另一方面，如果变量的生命周期是整个应用程序期间，它必须在任何函数体外声明。这些变量的内容在应用程序执行期间保持不变，并且可供所有内核使用。

我们将非数组的变量称为标量变量。如表 5.1 所示，所有在内核和设备函数中声明的自动标量变量都被放置到寄存器中。这些自动变量的作用域限定在单个线程内。当内核函数声明一个自动变量时，对于执行内核函数的每个线程，都会生成该变量的私有副本。当线程终止时，所有其自动变量都将不复存在。在图 5.1 中，变量 blurRow、blurCol、curRow、curCol、pixels 和 pixVal 都是自动变量，属于这个类别。请注意，访问这些变量非常快速和并行化，但必须小心不要超出硬件实现中寄存器存储的有限容量。使用大量寄存器可能会对每个 SM 的占用产生负面影响，正如我们在第 4 章，计算架构和调度中看到的那样。

自动数组变量不存储在寄存器中(这个规则也有一些例外情况。如果所有访问都是使用常量索引值完成的，编译器可能会决定将自动数组存储到寄存器中。)。相反，它们存储在线程的本地内存中，并可能产生长时间的访问延迟和潜在的访问拥塞。这些数组的作用域，就像自动标量变量一样，限定在单个线程内。也就是说，为每个线程创建并由每个线程使用自动数组的私有版本。一旦线程终止其执行，其自动数组变量的内容就会消失。根据我们的经验，很少需要在内核函数和设备函数中使用自动数组变量。

如果变量声明前带有 __shared__ 关键字（每个“__”由两个“_”字符组成），则它在 CUDA 中声明了一个共享变量。也可以在声明前面添加可选的 __device__ 来达到相同的效果。这样的声明通常在内核函数或设备函数中进行。共享变量驻留在共享内存中。共享变量的作用域在一个线程块内；也就是说，一个块内的所有线程看到同一个共享变量的版本。在内核执行期间，为每个块创建并使用共享变量的私有版本。共享变量的生命周期在内核执行期间。当内核终止其网格的执行时，共享变量的内容也将不复存在。正如我们之前讨论过的，共享变量是块内线程之间协作的有效手段。从共享内存中访问共享变量非常快速和高度并行化。CUDA 程序员通常使用共享变量来保存在内核执行阶段中经常使用和重复使用的全局内存数据的部分。可能需要调整用于创建执行阶段的算法，以便重点关注全局内存数据的小部分，就像我们将在第 5.4 节中通过矩阵乘法演示的那样。

如果变量声明前带有关键字 __constant（每个“__”由两个“_”字符组成），则它在 CUDA 中声明了一个常量变量。也可以在声明前面添加可选的 __device__ 来达到相同的效果。常量变量的声明必须在任何函数体外。常量变量的作用域是所有网格，这意味着所有网格中的所有线程看到同一个常量变量的版本。常量变量的生命周期是整个应用程序的执行期间。常量变量通常用于向内核函数提供输入值的变量。常量变量的值不能被内核函数代码更改。常量变量存储在全局内存中，但会进行缓存以实现高效访问。通过适当的访问模式，访问常量内存是非常快速和并行化的。目前，应用程序中常量变量的总大小限制为 65,536 字节。可能需要分割输入数据量以适应此限制。我们将在第 7 章，卷积中演示常量内存的使用。

如果变量声明仅由关键字 __device__（每个“__”由两个“_”字符组成）前置，那么它是一个全局变量，并将放置在全局内存中。访问全局变量的速度较慢。最近的设备中使用缓存提高了访问全局变量的延迟和吞吐量。全局变量的一个重要优势是它们对所有内核的所有线程可见。它们的内容也在整个执行期间持续存在。因此，全局变量可以用作跨块协作的手段。然而，必须注意，目前没有简单的方法可以在不使用原子操作或终止当前内核执行的情况下，在来自不同线程块的线程之间同步，或确保全局内存中的数据一致性。因此，全局变量通常用于将信息从一个内核调用传递到另一个内核调用。

在 CUDA 中，指针可以用于指向全局内存中的数据对象。指针在内核和设备函数中使用有两种典型方式。首先，如果一个对象是由主机函数分配的，那么该对象的指针将由内存分配 API 函数（如 cudaMalloc）初始化，并且可以作为参数传递给内核函数，正如我们在第 2 章，异构数据并行计算，和第 3 章，多维网格和数据中看到的那样。第二种使用方式是将在全局内存中声明的变量的地址分配给指针变量。例如，在内核函数中的语句 {float* ptr=&GlobalVar;} 将 GlobalVar 的地址分配给自动指针变量 ptr。读者应参考 CUDA 编程指南了解在其他内存类型中使用指针的方法。

5.3 减少内存访问的瓦片化(Tiling)

在CUDA中使用设备内存存在一个固有的权衡：全局内存容量大但速度慢，而共享内存容量小但速度快。一个常见的策略是将数据分割成称为瓦片的子集，以便每个瓦片都可以适应共享内存。瓦片一词来源于这样一个类比：一个大墙（即全局内存数据）可以由小瓦片（即每个都可以适应共享内存的子集）覆盖。一个重要的标准是，这些瓦片上的核心计算可以相互独立进行。请注意，并非所有数据结构都可以在任意的核函数中分割成瓦片。

图5.5 矩阵乘法的一个小例子。为了简洁起见，我们将M[y*Width+x]、N[y*Width+x]、P[y*Width+x]分别表示为$M_{y,x}、N_{y,x}、P_{y,x}$

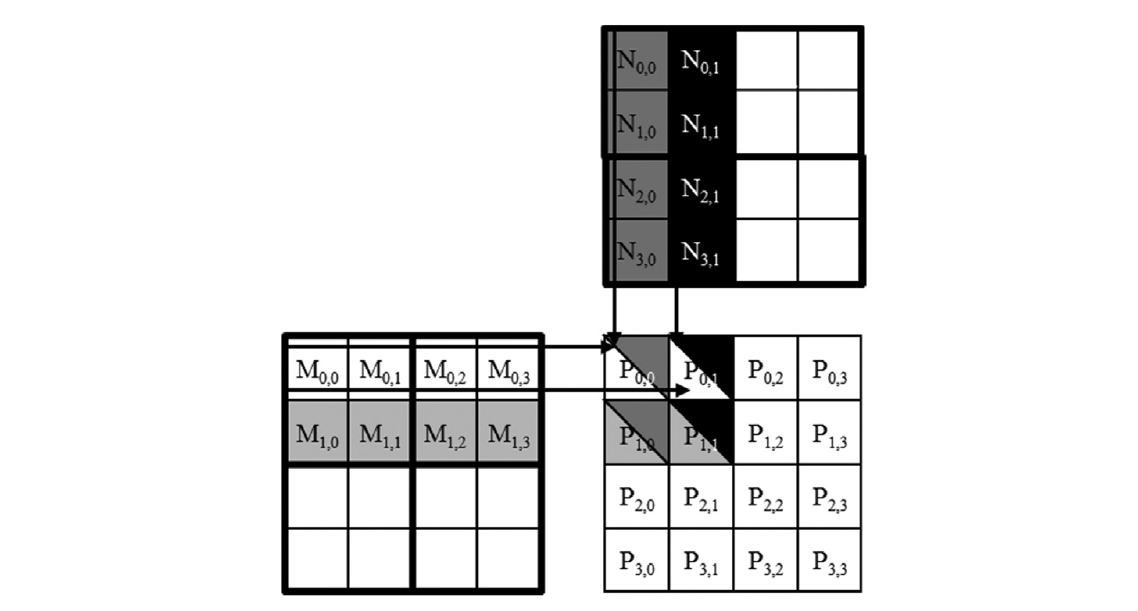
瓦片的概念可以通过第3章《多维网格和数据》中的矩阵乘法示例进行说明。图3.13展示了一个小型矩阵乘法示例。它对应于图3.11中的核函数。我们在图5.5中复制了该示例以便参考。为了简洁起见，我们将M[y*Width+x]、N[y*Width+x]、P[y*Width+x]分别表示为$M_{y,x}、N_{y,x}、P_{y,x}$。该示例假设我们使用四个2 x 2块来计算P矩阵。P矩阵中的粗框定义了每个块处理的P元素。图5.5突出显示了$\text{block}_{0,0}$的四个线程所做的计算。这四个线程计算$P_{0,0}、P_{0,1}、P_{1,0}和P_{1,1}$。线程0,0和线程0,1在block0,0中的M和N元素访问用黑色箭头标出。例如，线程0,0先读取M0,0和N0,0，然后是M0,1和N1,0，接着是M0,2和N2,0，最后是M0,3和N3,0。图5.6展示了block0,0中所有线程所做的全局内存访问。线程按垂直方向列出，水平方向的访问时间从左到右增加。请注意，每个线程在执行期间都会访问四个M元素和四个N元素。在突出显示的四个线程中，它们访问的M和N元素有很大的重叠。例如，线程0,0和线程0,1都访问了M0,0以及M的第0行的其余部分。类似地，线程0,1和线程1,1都访问了N0,1以及N的第1列的其余部分。

图5.6 $\text{block}_{0,0}$中线程执行的全局内存访问。

图3.11中的核函数编写得让线程0,0和线程0,1从全局内存中访问第0行的M元素。如果我们能够让线程0,0和线程0,1协作，使这些M元素仅从全局内存加载一次，我们就可以将对全局内存的总访问次数减半。实际上，我们可以看到在block0,0的执行过程中，每个M和N元素都被访问了两次。因此，如果我们可以让所有四个线程在访问全局内存时进行协作，我们就可以将对全局内存的流量减半。

读者应该验证在矩阵乘法示例中全局内存流量的潜在减少与所使用的块的维度成正比。对于Width × Width块，全局内存流量的潜在减少量将是Width。也就是说，如果我们使用16 x 16块，通过线程协作，我们可以将全局内存流量潜在地减少到原来的1/16。现在我们介绍一个瓦片矩阵乘法算法。基本思想是在各个线程在对点乘计算中独立使用这些元素之前，共同将M和N元素的子集加载到共享内存中。请注意，共享内存的大小非常有限，当将这些M和N元素加载到共享内存时，必须小心不要超出共享内存的容量。这可以通过将M和N矩阵划分成更小的瓦片来实现。这些瓦片的大小被选择为使其适合共享内存。在最简单的情况下，瓦片的维度等于块的维度，如图5.7所示。

图5.7 将M和N分块以利用共享内存。

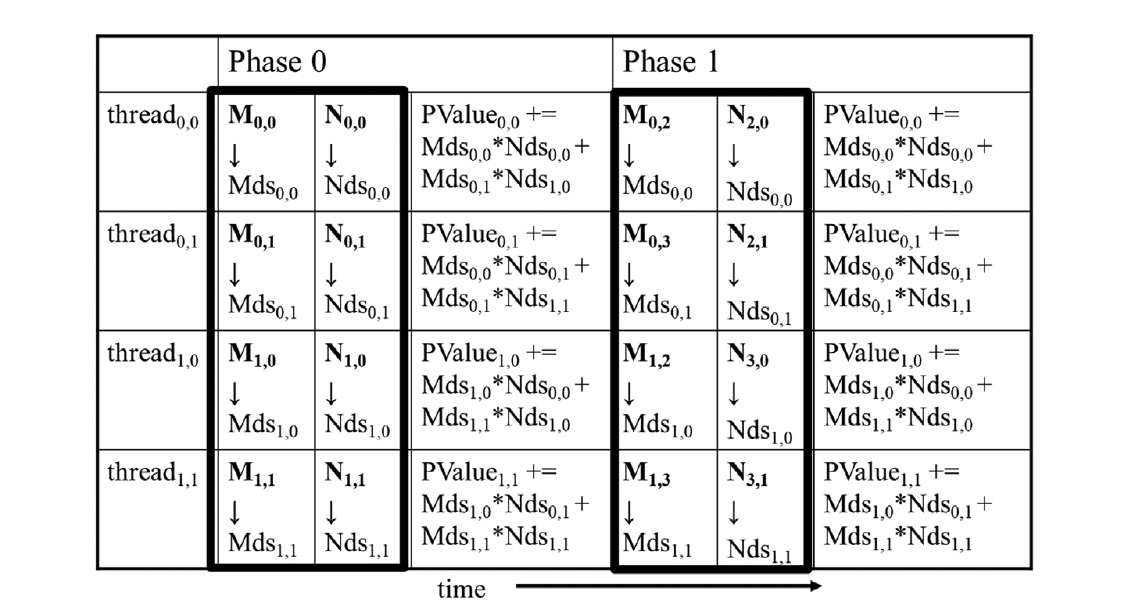
在图5.7中，我们将M和N分成了2 x 2的瓦片，由粗线划分。每个线程执行的点乘计算现在被分成了几个阶段。在每个阶段，块中的所有线程都协作将一个M瓦片和一个N瓦片加载到共享内存中。这可以通过让块中的每个线程将一个M元素和一个N元素加载到共享内存中来实现，如图5.8所示。图5.8的每一行显示了一个线程的执行活动。请注意，时间从左到右递增。我们只需要显示block0,0中线程的活动；其他块的行为都相同。用于M元素的共享内存数组称为Mds。用于N元素的共享内存数组称为Nds。在第1阶段开始时，block0,0的四个线程协作将一个M瓦片加载到共享内存中：线程0,0将M0,0加载到Mds 0,0中，线程0,1将M0,1加载到Mds 0,1中，线程1,0将M1,0加载到Mds 1,0中，线程1,1将M1,1加载到Mds 1,1中。这些加载操作显示在图5.8的第二列中。一个N瓦片也以类似的方式加载，显示在图5.8的第三列中。

图5.8 分块矩阵乘法的执行阶段。

在两个M和N瓦片加载到共享内存后，这些元素被用于点乘的计算。请注意，共享内存中的每个值都被使用了两次。例如，由线程1,1加载到Mds1,1中的M1,1值被线程1,0和线程1,1分别使用了一次。通过将每个全局内存值加载到共享内存中，使其可以被多次使用，我们减少了对全局内存的访问次数。在这种情况下，我们将全局内存的访问次数减少了一半。读者应该验证，如果瓦片是N x N元素，则减少的访问次数将是N的倍数。

还要注意，每个点乘的计算现在分成了两个阶段，在图5.8中分别表示为第1阶段和第2阶段。在每个阶段中，每个线程将输入矩阵元素的两对积累到Pvalue变量中。请注意，Pvalue是一个自动变量，因此为每个线程生成了一个私有版本。我们添加了下标只是为了说明这是为每个线程创建的不同实例的Pvalue变量。第1阶段的计算显示在图5.8的第四列中，第2阶段显示在第七列中。通常，如果输入矩阵的维度是Width，瓦片大小是TILE_WIDTH，则点乘将在Width/TILE_WIDTH个阶段中执行。创建这些阶段对于减少对全局内存的访问至关重要。由于每个阶段都专注于输入矩阵值的一个小子集，线程可以协作加载子集到共享内存，并使用共享内存中的值来满足在该阶段中的重叠输入需求。

还要注意，Mds和Nds在各个阶段之间被重用。在每个阶段中，相同的Mds和Nds被重用来保存用于该阶段的M和N元素的子集。这样一来，一个更小的共享内存就可以为大多数全局内存访问提供服务。这是因为每个阶段都专注于输入矩阵元素的一个小子集。这种专注的访问行为称为局部性。当算法表现出局部性时，就有机会使用小型高速存储器来服务大多数访问，并将这些访问从全局内存中删除。在多核CPU和多线程GPU中，实现高性能的关键在于局部性。我们将在第6章《性能考虑》中重新讨论局部性的概念。

5.4 使用分块矩阵乘法内核

现在我们准备介绍一个使用共享内存来减少对全局内存访问量的分块矩阵乘法内核。图5.9中显示的内核实现了图5.8中所示的阶段。在图5.9中，第4行和第5行分别声明了Mds和Nds为共享内存数组。回想一下，共享内存变量的作用域是一个块。因此，Mds和Nds数组的每个块都将创建一个版本，块的所有线程都可以访问相同的Mds和Nds版本。这一点很重要，因为块中的所有线程必须能够访问由其同行加载到Mds和Nds中的M和N元素，以便它们可以使用这些值来满足其输入需求。【本kernel函数只能处理WIDTH x WIDTH的两个方阵的乘法。】

图5.9 使用共享内存的分块矩阵乘法内核。

第7行和第8行将threadIdx和blockIdx的值保存到较短名称的自动变量中，以使代码更加简洁。回想一下，自动标量变量被放置在寄存器中。它们的作用域是在每个单独的线程中。也就是说，运行时系统为每个线程创建了tx、ty、bx和by的私有版本，并将其放置在线程可以访问的寄存器中。它们使用threadIdx和blockIdx的值进行初始化，并在线程的生命周期中使用多次。一旦线程结束，这些变量的值就会消失。

第11行和第12行分别确定了线程要生成的P元素的行索引和列索引。代码假定每个线程负责计算一个P元素。如第12行所示，线程要生成的P元素的水平（x）位置或列索引可以计算为bx * TILE_WIDTH+tx。这是因为每个块在水平维度上覆盖了TILE_WIDTH个P元素。块中的一个线程将在其前面有bx个块的线程，或者（bx * TILE_WIDTH）个线程；它们覆盖了bx * TILE_WIDTH个P元素。同一块中的另一个tx线程将覆盖另外tx个元素。因此，bx和tx的线程应负责计算x索引为bx * TILE_WIDTH+tx的P元素。例如，图5.7中，块1,0中的线程0,1要计算的P元素的水平（x）索引为0*2+1=1。这个水平索引保存在线程的变量Col中，也在图5.10中有所示。

类似地，由线程处理的P元素的垂直（y）位置或行索引被计算为by * TILE_WIDTH+ty。回到图5.7的示例，块1,0中的线程0,1要计算的P元素的y索引是1 * 2+0=2。这个垂直索引保存在线程的变量Row中。如图5.10所示，每个线程计算Colth列和Rowth行的P元素。因此，块1,0中的线程0,1要计算的P元素是P2,1。

图5.9的第16行标志着迭代计算P元素的所有阶段的循环的开始。循环的每次迭代对应于图5.8中所示的计算的一个阶段。ph变量表示已经完成的点积计算的阶段数。回想一下，每个阶段使用一个M和一个N元素的瓦片。因此，在每个阶段的开始时，前面的阶段已经处理了ph*TILE_WIDTH对M和N元素。

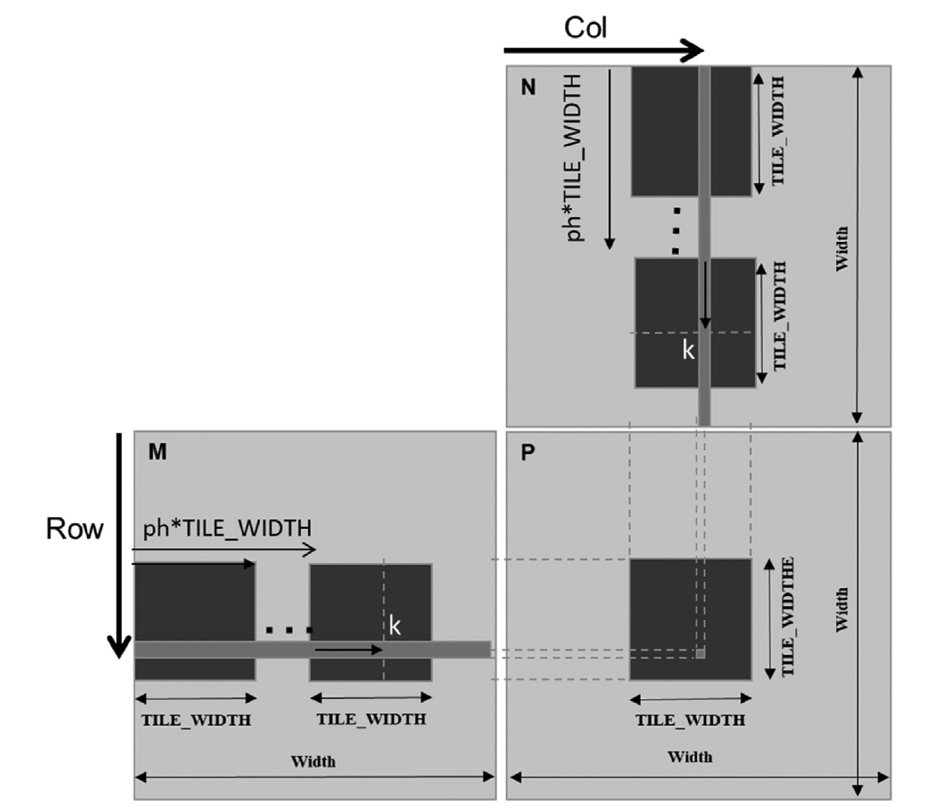
在每个阶段中，图5.9中的第19行和第20行加载相应的M和N元素到共享内存中。由于我们已经知道了要处理的M的行和N的列，现在我们将焦点转向了M的列索引和N的行索引。如图5.10所示，每个块有TILE_WIDTH个线程将协作加载TILE_WIDTH个M元素和TILE_WIDTH个N元素到共享内存中。因此，我们只需要将每个线程分配给加载一个M元素和一个N元素。通过使用blockIdx和threadIdx，这可以很方便地实现。注意，要加载的M元素部分的开始列索引是ph * TILE_WIDTH。因此，一个简单的方法是让每个线程加载离该开始点tx（threadIdx.x的值）位置的元素。类似地，要加载的N元素部分的开始行索引也是ph * TILE_WIDTH。因此，每个线程加载离该开始点ty（threadIdx.y的值）位置的元素。

图5.10 分块乘法中矩阵索引的计算。

这正是我们在第19和20行所做的。在第19行，每个线程加载M[Row * Width + ph * TILE_WIDTH + tx],，其中线性化索引由行索引Row和列索引ph * TILE_WIDTH + tx形成。由于Row的值是ty的线性函数，因此$\text{TILE_WIDTH}^2$个线程将分别加载唯一的M元素到共享内存中，因为每个线程具有独特的tx和ty组合。这些线程一起将在图5.10中加载M的一个黑色方块子集。类似地，在第20行，每个线程使用线性化索引(ph * TILE_WIDTH + ty) * Width + Col将适当的N元素加载到共享内存中。读者应该使用图5.7和5.8中的小例子来验证地址计算是否正确适用于各个线程。

第21行中的屏障__syncthreads()确保所有线程在任何一个线程继续之前都已经完成了M和N的瓦片加载到Mds和Nds中。回顾第4章，计算架构和调度，可以调用__syncthreads()使块中的所有线程等待其他线程到达屏障之前，它们无法继续执行。这很重要，因为其他线程可以加载线程需要使用的M和N元素。需要确保所有元素都正确加载到共享内存中，然后任何线程才能开始使用这些元素。然后，第23行中的循环执行了一个点积的阶段。线23的循环变量k表示每个线程的dot product的阶段。请注意，这些元素将从保存这些M和N元素的共享内存数组Mds和Nds中访问。第26行中的屏障__syncthreads()确保所有线程在移动到下一个迭代并从下一个瓦片加载元素之前，所有线程都已经完成使用共享内存中的M和N元素。因此，没有一个线程会提前加载元素并破坏其他线程的输入值。

第21行和第26行中的两个__syncthreads()调用展示了并行程序员在协调线程之间时经常必须考虑的两种不同类型的数据依赖关系。第一种称为写后读(read-after-write)依赖，因为线程必须等待其他线程将数据写入到正确位置后才能尝试读取。第二种称为读后写(write-after-read)依赖，因为线程必须等待所有需要的数据被所有线程读取后才能进行写入。写后读和读后写依赖的其他名称分别是真依赖和假依赖。写后读依赖是真依赖，因为读取线程确实需要写入线程提供的数据，因此它别无选择，只能等待。读后写依赖是假依赖，因为写入线程不需要读取线程的任何数据。这种依赖关系是由于它们重用相同的内存位置造成的，并且如果它们使用不同的位置，则不会存在。

从第16行到第28行的循环嵌套展示了一种称为分块（strip mining）的技术，该技术将长时间运行的循环分解成阶段。每个阶段涉及内部循环，该内部循环执行原始循环的一些连续迭代。原始循环成为外部循环，其作用是按顺序迭代地调用内部循环，以便执行原始循环的所有迭代。通过在内部循环之前和之后添加屏障同步，我们强制同一块中的所有线程在每个阶段都集中精力处理同一部分输入数据。分块是在数据并行程序中创建所需阶段的重要手段。

完成所有点积阶段后，执行退出外部循环。在第29行，所有线程使用从Row和Col计算得到的线性化索引写入其P元素。分块算法的好处是巨大的。对于矩阵乘法，全局内存访问量减少了TILE_WIDTH倍。使用16x16的瓦片，可以将全局内存访问量减少16倍。这将计算与全局内存访问的比率从0.25 OP/B提高到4 OP/B。这种改进使CUDA设备的内存带宽能够支持更高的计算速率。例如，在A100 GPU中，其全局内存带宽为1555 GB/秒，这种改进使设备可以达到(1555 GB/秒) * (4 OP/B) = 6220 GFLOPS，远高于未使用分块的内核实现的389 GFLOPS。

尽管分块大大提高了吞吐量，6220 GFLOPS仍然只是设备峰值吞吐量19500 GFLOPS的32%。可以进一步优化代码以减少全局内存访问次数并提高吞吐量。我们将在本书的后面看到其中一些优化，而其他高级优化将不会涵盖。由于矩阵乘法在许多领域中都非常重要，因此有高度优化的库，如cuBLAS和CUTLASS，已经包含了许多这些高级优化。程序员可以使用这些库立即在其线性代数应用程序中实现接近峰值性能。

分块矩阵乘法内核提高了矩阵乘法特别是应用程序的吞吐量，这并不是GPU独有的。长期以来，在CPU上应用分块（或阻塞）技术以提高性能有着悠久的历史，它确保了CPU线程在特定时间窗口内重复使用的数据将在缓存中找到。一个关键区别是，CPU上的分块技术依赖于CPU缓存隐式地将重复使用的数据保存在芯片上，而GPU上的分块技术使用共享内存显式地将数据保存在芯片上。原因是CPU核心通常一次运行一个或两个线程，因此一个线程可以依赖于缓存保持最近使用的数据。相比之下，GPU SM同时运行许多线程以隐藏延迟。这些线程可能会竞争缓存槽，这使得GPU缓存不太可靠，因此需要使用共享内存来保存要重复使用的重要数据。

虽然分块矩阵乘法内核的性能提高令人印象深刻，但它确实做出了一些简化假设。首先，假定矩阵的宽度是线程块的宽度的倍数。这防止了内核正确处理具有任意宽度的矩阵。第二个假设是矩阵是方阵。在实践中，这并不总是正确的。在下一节中，我们将介绍一个带有边界检查的内核，以消除这些假设。

5.5 边界检查

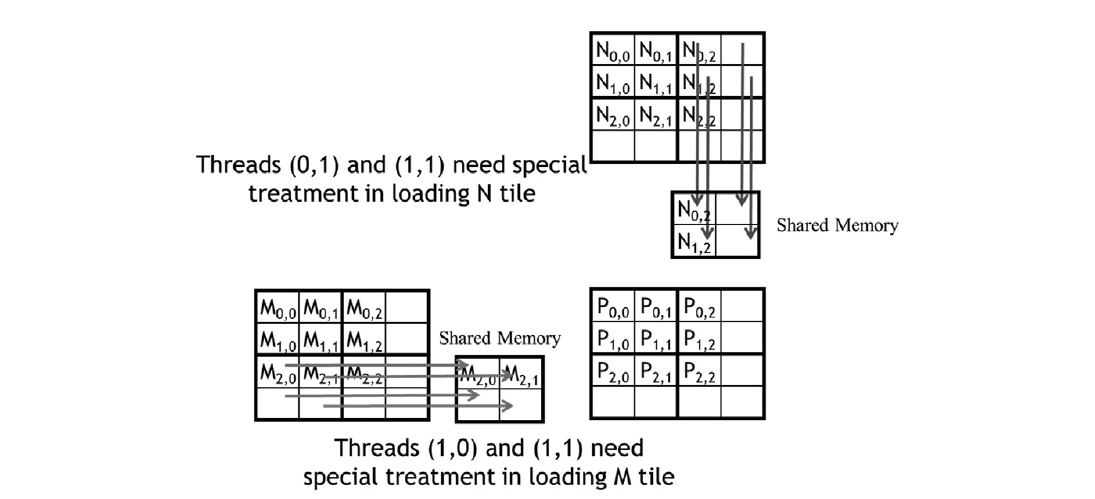
现在我们将扩展分块矩阵乘法内核以处理具有任意宽度的矩阵。这些扩展将允许内核正确处理宽度不是瓦片宽度的倍数的矩阵。让我们将图5.7中的小例子改为使用3x3的M、N和P矩阵。修订后的例子如图5.11所示。请注意，矩阵的宽度为3，不是瓦片宽度（为2）的倍数。图5.11显示了第0块0,0的第二阶段的内存访问模式。我们看到线程0,1和线程1,1将尝试加载不存在的M元素。同样，我们看到线程1,0和线程1,1将尝试访问不存在的N元素。

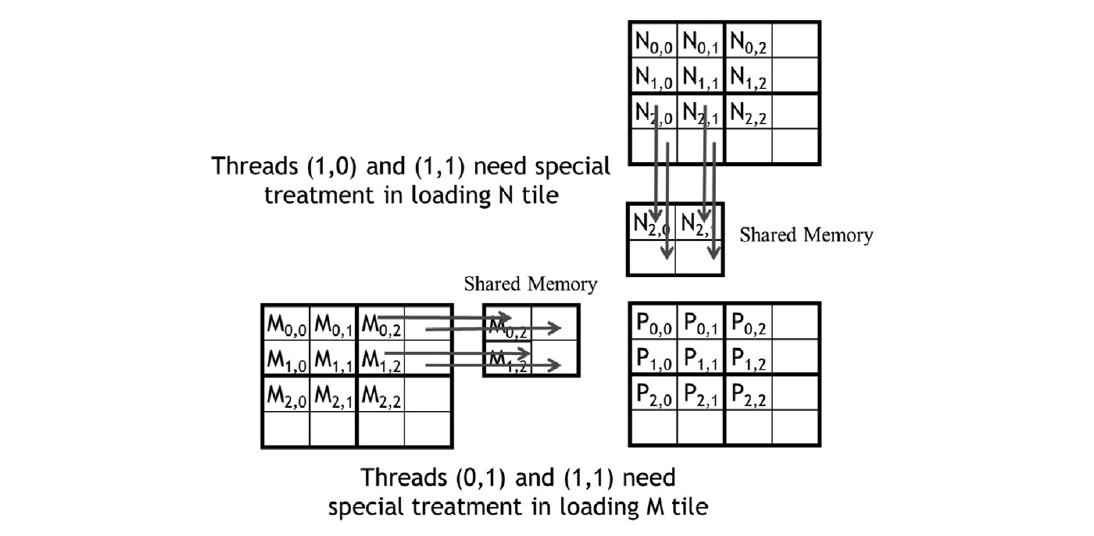图5.11 加载靠近边缘的输入矩阵元素：块0,0的第1阶段。

访问不存在的元素有两个问题。对于访问超出行末端的不存在元素的情况（如图5.11中的线程0,1和线程1,1的M访问），这些访问将被用于不正确的元素。在我们的例子中，线程将尝试访问M0,3和M1,3，这些元素不存在。那么这些内存加载会发生什么？为了回答这个问题，我们需要回到二维矩阵的线性布局。在M0,2之后的元素在线性布局中是M1,0。虽然线程0,1正试图访问M 0,3，但它最终会得到M1,0。在随后的内积计算中使用此值显然会破坏输出值。

在访问超出列末端的元素的情况下（如图5.11中的线程1,0和线程1,1的N访问），会出现类似的问题。这些访问是对数组分配区域外的内存位置的访问。在某些系统中，它们将从其他数据结构返回随机值。在其他系统中，这些访问将被拒绝，导致程序中止。无论哪种方式，这些访问的结果都是不可取的。

到目前为止，从我们的讨论来看，问题访问似乎只在线程执行的最后一个阶段中出现。这可能表明我们可以在分块内核执行的最后阶段采取特殊的操作来处理它。不幸的是，这并不正确。问题访问可能在所有阶段中出现。图5.12显示了第1块1,1在阶段0期间的内存访问模式。我们看到线程1,0和线程1,1试图访问不存在的M元素M3,0和M3,1，而线程0,1和线程1,1试图访问不存在的N0,3和N1,3。

图5.12 加载块1,1的第0阶段的输入元素

请注意，这些问题访问无法通过简单地排除不计算有效P元素的线程来预防。例如，第1块1,1中的线程1,0不计算任何有效的P元素。然而，它需要在阶段0中加载M2,1，以供第1块1,1中的其他线程使用。此外，请注意，一些计算有效P元素的线程将尝试访问不存在的M或N元素。例如，正如我们在图5.11中看到的，块0,0中的线程0,1计算一个有效的P元素P0,1。然而，它在阶段1中尝试访问不存在的M0,3。这两个事实表明，我们需要使用不同的边界条件测试来加载M瓦片、加载N瓦片和计算/存储P元素。一个可以遵循的经验法则是，每个内存访问都需要相应的检查，以确保访问中使用的索引在所访问的数组的边界内。

我们从加载输入瓦片的边界测试条件开始。当一个线程要加载输入瓦片元素时，它应该测试它试图加载的输入元素是否是有效的元素。这可以通过检查y和x索引来轻松完成。例如，在图5.9的第19行中，线性化索引派生自行索引Row和列索引ph * TILE_WIDTH + tx。边界条件测试是，这两个索引都小于Width：Row < Width && (ph * TILE_WIDTH + tx) < Width。如果条件为真，则线程应继续加载M元素。读者应该验证加载N元素的条件测试是（ph * TILE_WIDTH + ty） < Width && Col < Width。

如果条件为假，则线程不应加载该元素。问题是应该将什么放入共享内存位置。答案是0.0，这是一个不会在内积计算中造成任何伤害的值。如果任何线程在其内积计算中使用这个0.0值，那么内积值不会发生任何变化。

最后，只有在负责计算有效P元素时，线程才应存储其最终内积值。此条件的测试是(Row < Width)&& (Col < Width)。带有额外边界条件检查的内核代码如图5.13所示。

图5.13 带有边界条件检查的分块矩阵乘法核心。

经过边界条件检查，分块矩阵乘法核心距离成为通用矩阵乘法核心仅一步之遥。通常，矩阵乘法定义适用于矩形矩阵：一个 j 乘 k 的 M 矩阵与一个 k 乘 l 的 N 矩阵相乘得到一个 j 乘 l 的 P 矩阵。到目前为止，我们的核心只能处理方阵。

幸运的是，将我们的核心进一步扩展为通用矩阵乘法核心相当容易。我们需要做一些简单的修改。首先，将 Width 参数替换为三个无符号整数参数：j、k、l。在用于引用 M 的高度或 P 的高度的地方，将 Width 替换为 j。在用于引用 M 的宽度或 N 的高度的地方，将 Width 替换为 k。在用于引用 N 的宽度或 P 的宽度的地方，将 Width 替换为 l。对这些更改后的核心的修改留作练习。

5.6 内存使用对占用率的影响

回顾第四章《计算架构与调度》，我们讨论了最大化 SM 上线程的占用率的重要性，以便能够容忍长延迟操作。核心的内存使用在占用率调优中起着重要作用。虽然 CUDA 寄存器和共享内存可以极大地减少对全局内存的访问次数，但必须小心谨慎地控制这些内存的使用量，以保持在 SM 的容量范围内。每个 CUDA 设备都提供有限的资源，这限制了对于给定应用程序，可以同时驻留在 SM 中的线程数量。一般来说，每个线程需要的资源越多，每个 SM 中可以驻留的线程数量就越少。

我们在第四章《计算架构与调度》中看到，寄存器的使用量可能是占用率的一个限制因素。共享内存的使用量也可能限制可以分配给每个 SM 的线程数量。例如，A100 GPU 的每个 SM 最多可以配置为具有 164 KB 的共享内存，并支持每个 SM 的最大线程数为 2048 个。因此，为了使用所有 2048 个线程槽位，一个线程块不应该使用超过平均值为 (164 KB) / (2048 个线程) = 82 B/线程的共享内存。在分块矩阵乘法示例中，每个块有 2 × 2 × TILE_WIDTH 个线程，并且为 Mds 使用 TILE_WIDTH × 4B 的共享内存，为 Nds 使用 2 × TILE_WIDTH × 4B 的共享内存。因此，线程块使用的平均共享内存为 ($\text{TILE_WIDTH}^2$ × 4B + $\text{TILE_WIDTH}^2$ × 4B) / ($\text{TILE_WIDTH}^2$ 个线程) = 8 B/线程。因此，分块矩阵乘法核心的占用率不受共享内存的限制。

然而，考虑一个线程块使用 32 KB 共享内存，每个线程块有 256 个线程的核心。在这种情况下，该核心使用的平均共享内存为 (32 KB) / (256 个线程) = 132 B/线程。使用这样的共享内存使用量，核心无法实现完整的占用率。每个 SM 最多可以承载 (164 KB) / (132 B/线程) = 1272 个线程。因此，该核心的最大可达到的占用率将是 (1272 个分配的线程) / (2048 个最大线程) = 62%。

需要注意的是，每个 SM 中共享内存的大小也可能因设备而异。每一代或型号的设备可以具有不同数量的共享内存。通常情况下，希望核心能够根据硬件中可用的共享内存量使用不同的共享内存量。也就是说，我们可能希望主机代码能够动态确定共享内存的大小，并调整核心使用的共享内存量。可以通过调用 cudaGetDeviceProperties 函数来实现这一点。假设变量 &devProp 传递给函数。在这种情况下，字段 devProp.sharedMemPerBlock 给出每个 SM 中可用的共享内存量。程序员然后可以确定每个块应该使用的共享内存量。

不幸的是，图 5.9 和图 5.13 中的核心不支持由主机代码动态调整共享内存使用量。在图 5.9 中使用的声明将其共享内存使用量硬编码为编译时常量：

__shared__ float Mds[TILE_WIDTH][TILE_WIDTH];
__shared__ float Nds[TILE_WIDTH][TILE_WIDTH];

#define TILE_WIDTH 16

也就是说，无论在编译时将 TILE_WIDTH 设置为何值，Mds 和 Nds 的大小都被设置为 $\text{TILE_WIDTH}^2$ 个元素。由于代码包含了 Mds 和 Nds，它们都将拥有 256 个元素。如果我们想要改变 Mds 和 Nds 的大小，我们需要改变 TILE_WIDTH 的值并重新编译代码。在不重新编译的情况下，核心不能轻松地在运行时调整其共享内存使用量。

我们可以通过在 CUDA 中使用不同的声明样式来启用这种调整，通过在共享内存声明前添加一个 C extern 关键字并在声明中省略数组的大小。基于这种样式，Mds 和 Nds 的声明需要合并为一个动态分配的数组：

extern __shared__ Mds_Nds[];

由于只有一个合并的数组，我们还需要手动定义数组的 Mds 部分和 Nds 部分的起始位置。请注意，合并的数组是一维的。我们需要使用基于垂直和水平索引的线性化索引来访问它。

在运行时，当我们调用核心时，我们可以根据设备查询结果动态配置每个块使用的共享内存量，并将其作为第三个配置参数提供给核心调用。例如，修订后的核心可以使用以下语句启动：

其中 size_t 是一个内置类型，用于声明变量以保存动态分配的数据结构的大小信息。大小以字节为单位表示。在我们的矩阵乘法示例中，对于一个 16 乘 16 的瓦片，我们有一个大小为 2 乘 16 乘 16 乘 4 = 2048 字节来容纳 Mds 和 Nds。我们省略了在运行时设置 size 值的计算细节，并将其作为读者的练习留下。

在图 5.14 中，我们展示了如何修改图 5.9 和图 5.11 中的核心代码，以使用动态大小的共享内存来存储 Mds 和 Nds 数组。将每个数组部分的大小作为参数传递给核心函数可能也很有用。在这个例子中，我们添加了两个参数：第一个参数是 Mds 部分的大小，第二个参数是 Nds 部分的大小，都以字节为单位。请注意，在上述主机代码中，我们将 size/2 作为这些参数的值，即 1024 字节。通过第 06 和 07 行的赋值，核心代码的其余部分可以使用 Mds 和 Nds 作为数组的基础，并使用线性化索引来访问 Mds 和 Nds 元素。例如，不使用 Mds[ty][tx]，而是使用 Mds[ty * TILE_WIDTH+tx]。

图5.14 具有动态大小共享内存使用的瓦片矩阵乘法核心。

5.7 总结

总的来说，现代处理器上程序的执行速度可能会受到内存速度的严重限制。要实现对 CUDA 设备执行吞吐量的良好利用，就需要在内核代码中努力实现高的计算与全局内存访问比率。如果比率较低，那么内核就会受到内存限制，即其执行速度受限于操作数从内存中访问的速率。

CUDA 提供对寄存器、共享内存和常量内存的访问。这些内存比全局内存小得多，但可以以更高的速度访问。要有效地使用这些内存，就需要重新设计算法。我们以矩阵乘法为例，说明了瓦片化是增强数据访问局部性并有效利用共享内存的一种流行策略。在并行编程中，瓦片化使用屏障同步来强制多个线程在执行的每个阶段联合关注输入数据的一个子集，以便将子集数据放入这些特殊的内存类型中，从而实现更高的访问速度。

然而，CUDA 程序员需要注意这些特殊类型内存的有限大小。它们的容量取决于具体的实现。一旦超出了它们的容量，它们就会限制每个 SM 中可以同时执行的线程数量，并可能对 GPU 的计算吞吐量以及其耐受延迟的能力产生负面影响。在开发应用程序时考虑硬件限制的能力是并行编程的一个关键方面。

尽管我们是在 CUDA C 编程的背景下介绍了瓦片化算法，但它是在几乎所有类型的并行计算系统中实现高性能的有效策略。原因在于应用程序必须表现出数据访问的局部性，以便在这些系统中有效利用高速内存。例如，在多核 CPU 系统中，数据局部性可以使应用程序有效地使用芯片内数据缓存，从而降低内存访问延迟并实现高性能。这些芯片内数据缓存也具有有限的大小，并且需要计算表现出局部性。因此，当开发其他类型的并行计算系统的并行应用程序时，读者也会发现瓦片化算法很有用，使用其他编程模型。

本章的目标是介绍局部性、瓦片化以及不同的 CUDA 内存类型的概念。我们介绍了使用共享内存的瓦片矩阵乘法核心。我们进一步研究了需要边界测试条件来允许在应用瓦片化技术时处理任意数据维度的需求。我们还简要讨论了动态大小的共享内存分配的使用，以便内核可以根据硬件能力调整每个块使用的共享内存大小。我们没有讨论在瓦片化中使用寄存器。在本书第二部分讨论并行算法模式时，我们将解释在瓦片化算法中使用寄存器的情况。