本文介绍基于WFST的语音识别解码器算法,主要是静态的解码算法。
目录
本文介绍把WFST用于语音识别的更多细节内容。首先我们简要的介绍基于WFST的语音识别系统,然后解释语音识别系统的不同模块怎么用WFST来表示以及怎么把这些WFST组织成单一的搜索网络。最后我们介绍使用完全复合后的WFST来进行识别的时间同步Viterbi Beam搜索算法。
基于WFST的解码器的概览
WFST提供里一个统一的形式来表示当前SOTA的大规模连续语音识别(LVCSR)系统的不同知识源(knowledge source),比如HMM、声学模型、发音词典和N-gram语言模型。表示不同知识源的多个WFST可以通过复合运算整合成一个WFST,这个WFST表示的搜索网络的输入是HMM状态。然后这个WFST可以通过前面介绍的各种优化运算来去掉其中的冗余部分而变成等价的但是更加紧凑高效的WFST来加速解码过程。这里我们来简单的介绍一下基于WFST的语音识别系统的基本原理。
如前文介绍的,连续语音识别定义为在给定的输入语音信号O的条件下寻找最可能的词序列$\hat{W}$。似然可以使用贝叶斯公式变成$P(O \vert W)P(W)$,其中$P(W)$是语音模型的概率,而$P(O \vert W)$是声学模型概率。更具体的,通过发音词典引入发音概率$P(V \vert W)$,它表示给定词序列W的条件下phone序列V的概率。这3个概率分别通过声学模型、发音模型(词典)和语言模型来计算。因此前面的公式可以重写为:
\[\begin{split} \hat{W} &= \underset{W \in \mathcal{W}}{argmax} \sum_{V \in R(W)} P(O|V,W)P(V|W)P(W) \\ & \approx \underset{W \in \mathcal{W}}{argmax} \left \{ \sum_{V \in R(W)} P(O|V)P(V|W)P(W) \right \} \end{split}\]这里的$P(O \vert V)$、$P(V \vert W)$和$P(W)$分别通过声学模型、发音词典和语言模型来计算。W是所有可能的词序列而R(W)是词序列W的所有可能发音的phone的序列。因为目前SOTA的LVCSR系统都使用子词单元的声学模型,因此声学似然$P(O \vert V,W)$被假设只依赖于phone的序列从而近似为$P(O \vert V)$。
为了实现方便,在Viterbi解码器里我们使用log运算来替代乘法。解码器会进行如下的搜索:
\[\begin{split} \hat{W} & \approx \underset{W \in \mathcal{W}}{argmax} \left \{\sum_{V \in R(W)} P(O|V)P(V|W)P(W) \right \} \\ & = \underset{W \in \mathcal{W}}{argmax} \left \{\max_{V \in R(W)} log P(O|V) + logP(V|W)+logP(W) \right \} \end{split}\]在上面的公式里,因为是Viterbi近似,所以把求和变成了求最大值。为了简单,后面我们把对数似然和对数概率称为得分。$log P(O \vert V)$称为声学得分,$log P(V \vert W)$称为发音得分,$logP(W)$称为语言得分。WFST框架为我们提供里一种快速计算上式的方法。
在WFST框架里,语音识别问题被当作把输入语音信号O转换成词序列W的一个转换(transduction)过程。语音识别系统中的每一个模型都被解释为一个WFST,而模型的得分的取反(-log概率)被作为WFST的weight。对于上式的声学模型、发音词典和语言模型,我们分别定义H、L和G这3个WFST来表示它们。其中H把观察序列转换成phone序列V,其中$w_H(O \rightarrow V)=-logP(O \vert V)$;L把phone序列V转换成词序列W,其中$w_L(V \rightarrow W)=-logP(V \vert W)$;最后G把词序列W还是转换成W(G可以看成一个WFSA,它的作用是计算词序列W的概率,如果不接受可以认为概率是0),其中$w_G(W \rightarrow W)=-logP(W)$。然后从观察序列O到词序列W的变换就是先后通过H、L和G计算得到。为了计算效率,我们可以提前把H、L和G使用复合运算组合成一个WFST来直接把观察序列O转换成词序列W:
\[N=H \circ L \circ G\]上式中$\circ$是复合运算。因此,语音识别的过程被变成在N上搜索最小weight(因为是-log概率)的词序列:
\[\begin{split} \hat{W} & \approx \underset{W \in \mathcal{W}}{argmax} \left \{\max_{V \in R(W)} log P(O|V) + logP(V|W)+logP(W) \right \} \\ & = \underset{W \in \mathcal{W}}{argmax} \left \{\min_{V \in R(W)} (-log P(O|V)) + (-logP(V|W))+(-logP(W)) \right \} \\ & = \underset{W \in \mathcal{W}}{argmax} \left \{\min_{V \in R(W)} w_H(O \rightarrow V) \bigotimes w_L(V \rightarrow W) \bigotimes w_G(W \rightarrow W) \right \} \\ & = \underset{W \in \mathcal{W}}{argmax} \; w_N(O \rightarrow W) \end{split}\]上式我们假设weight是定义在热带半环上的,所以+就是$\bigotimes$。
当前SOTA的系统都是triphone的模型,为了实现triphone,我们加入一个额外的WFST C,这个WFST的作用是把triphone序列转换成phone序列:
\[N=H \circ C \circ L \circ G\]上面复合得到一个包含所有模型的搜索网络,其中跨词(cross-word)的triphone模型被完美的融入其中,这对于非WFST的传统解码方法来说是非常难以处理的。复合后的WFST可以使用前面介绍的各种WFST优化运算,比如确定化和最小化来进一步优化。这些优化运算可以在整个搜索网络(包含声学模型、发音词典和语言模型)上来进行优化,而传统的解码器优化通常被局限于某一个模型上。
只要复合的WFST构建完毕,解码器的工作就是对于给定的语音输入搜索最优的路径。如果模型没有发生变化,则WFST不需要更新。因此,WFST的解码器可以专注于使用优化的静态搜索网络来搜索最优路径;而传统的解码器通常是在非全局最优的搜索网络上进行搜索,而且因为内存等限制只能构造部分网络,在解码时还需要动态的扩展搜索网络。这是WFST的框架相对于传统方法的最重要的优点。此外,因为解码器被设计得可以处理任何WFST,所以解码器程序于具体的用WFST来表示的模型是无关的。这也是WFST框架的另一个好处——它让解码器更加通用和易于维护。
在后续的内容里,我们会介绍怎么构建语音识别系统中的各个模型的WFST,用于构建完整的复合WFST的一些常见复合和优化步骤以及使用WFST来解码的算法。如前面所述,基于WFST的语音识别系统把语音识别问题看成一个从输入语音观察序列到词序列的一个转换问题。但是我们需要注意:语音识别的转换问题其实是超出里WFST的定义。对于传统的语音识别系统,语音信号被转换成实数值的特征向量的序列。实数是连续的无穷的,因为WFST要求输入符号是有限的符号集合,所以无法用一个WFST把特征向量序列变成HMM状态序列。此外,给定一个HMM状态,计算观察向量的概率也是需要使用GMM模型on-the-fly的来计算,因此即使我们的WFST可以输入实数,它的weight和输入的关系也不是就简单对应关系,它需要根据概率密度函数公式来计算。因此,基于WFST的解码器会分成两部分,一部分处理连续的输入特征向量序列,而另一部分处理WFST。读者在后面的介绍里会更加清楚这一点。
语音识别系统各个部件(模型)的WFST构建
在本节,我们会介绍怎么用WFST来表示语音识别系统的不同部件,包括声学模型、phone上下文、发音词典和语言模型。具体来讲,我们着重关注语音识别中的标准模型,比如HMM模型、triphone上下文、简单的非概率的发音词典和n-gram语言模型。
声学模型(H)
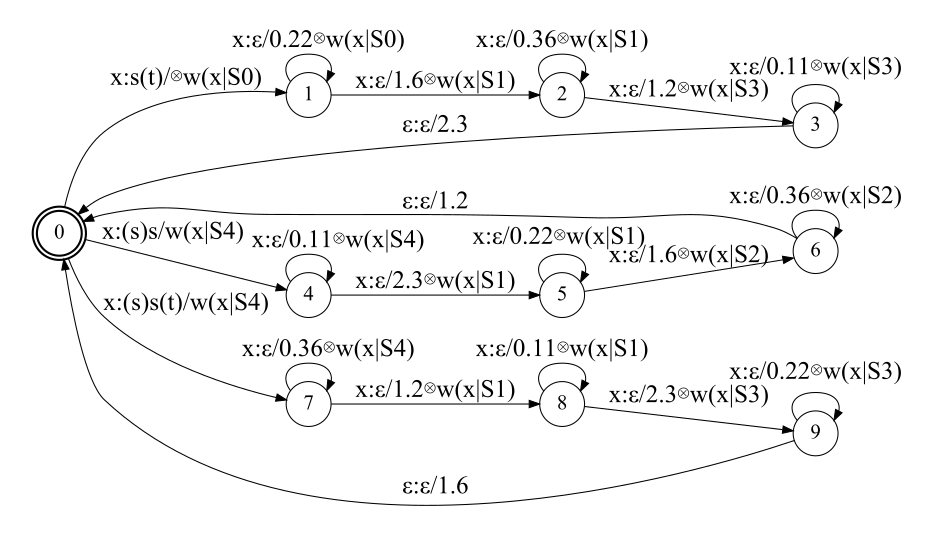
在基于WFST的方法里,一些声学模型可以被看成一个转换机(transducer),它把输入语音信号转化成一个(上下文相关的)phone序列,同时weight表示声学似然。下图是一个”假想”的上下文相关的HMM转换机。
上图的WFST里,包含了3个上下文相关的phone——s(t)、(s)s和(s)s(t)。其中(s)s(t)表示中心的phone是s,它的左边是s右边是t。而s(t)表示s的右边是t(没有左边的phone,因此它是一个开始的phone),(s)s表示s的左边是s,而右边没有phone。这3个上下文相关的phone都是从左到右的3状态的HMM,每个状态可以跳转到自己,也可以跳转到下一个状态。x是一个特殊的符号,它代表任意的输入特征向量。”x : s(t)/w(x|S0)”代表对于任意的输入特征向量x,WFST都可以从状态0跳转到状态1,并且输出是s(t),weight是函数x(x|S0),这里的”S0”表示第0个共享的状态。所有共享的状态的发射概率$b_{S_k}(x)$都是一样的。对于热带半环或者log半环,w(x|Sk)等于$-logb_{S_k}(x)$。除了从状态0开始的跳转,其它的跳转的输出符号都是ε,weight除了发射概率还包含状态的跳转概率(-log)。比如状态1的自跳转的weight为0.22 ⊗ w(x|S0),这里的0.22是状态自跳转的-log概率,因此真正的自跳转概率是0.8$(e^{-0.22}=0.8)$。⊗代表热点半环或者log半环上的乘法,因此从状态1到状态1的自跳转weight包含自跳转和发射概率的”相乘”。因此这个WFST的输入是声学特征,输出是上下文相关的phone。注意,这个WFST不考虑怎么把上下文相关的phone变成上下文无关的phone,那是后面介绍的C需要考虑的内容。
另外我们看一下哪些是共享的状态。比如(s)s和(s)s(t)的第一个状态(4和7)是共享的,因为它们的第一个状态都表示s的左边上下文是s,因此状态4和状态7的发射概率是相同的(但是跳转概率是不同的),在图中都用w(x|S4)表示。类似的,s(t)和(s)s(t)的最后一个状态也是共享的,因为它们的右边上下文是t。
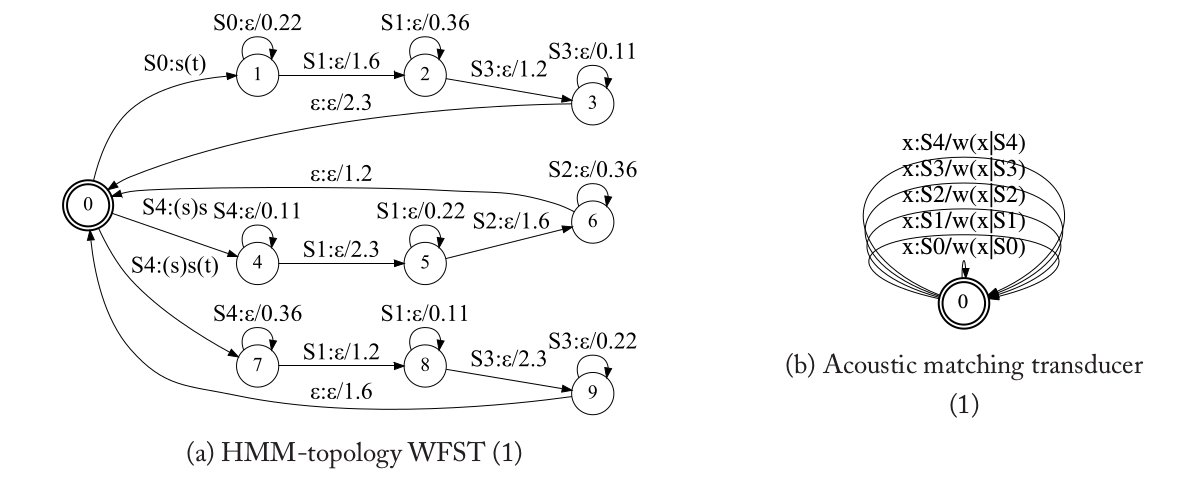
但是这里的转换机并不是真正的WFST,因此不能直接在WFST的框架里用标准的WFST来表示H。原因在于WFST要求输入是有限的离散符号,但是这里的输入是连续的无穷的实数值的向量。因此这里我们需要引入一个特殊的符号x和一个weight函数$w(x \vert S_k)$。为了解决这个问题,H被分解为两个部分——HMM拓扑结构和声学匹配(acoustic matching)。前者可以使用标准的WFST来处理,而后者是用解码器程序里的特殊代码来处理。下图是上图的H的一种分解方式。
在这种分解方式里,代表拓扑结构的WFST编码了HMM的状态和状态的跳转概率,而声学匹配部分处理特殊的符号x以及发射概率$w(x \vert S_k)$,它们的复合就得到了前面的H。读者可以自行验证一下它们的复合确实是H,从而更好的理解分解。
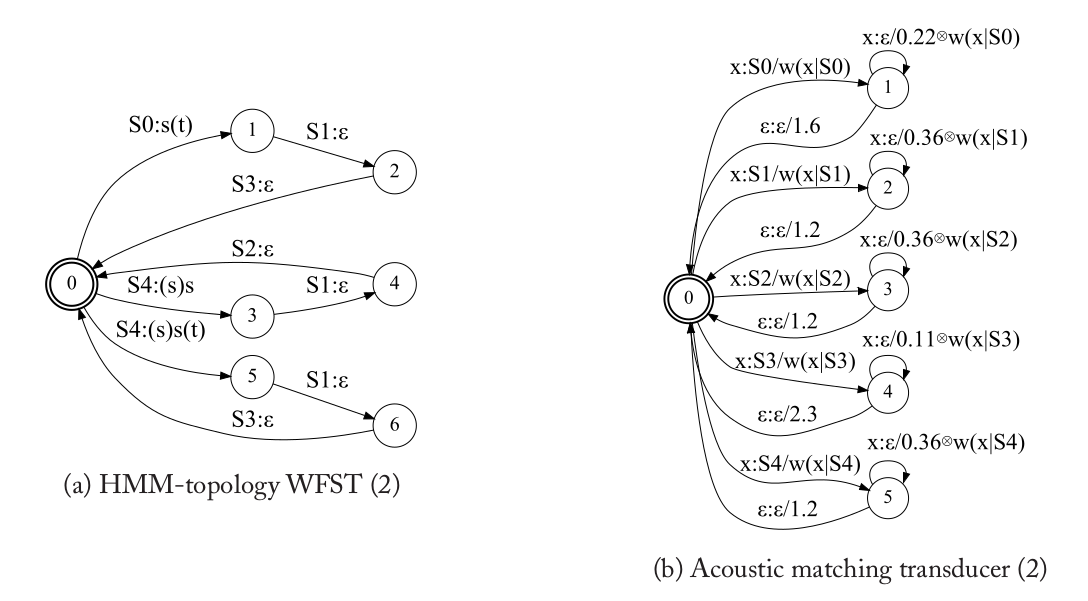
除此之外还有别的分解方式,比如下图。
在这种分解里,HMM拓扑结构只编码里每个phone的3个状态的顺序关系。状态转移概率都编码到声学匹配的WFST里了。比如我们看左边,它可以把输入符号序列”S0,S1,S3”转换成”s(t)”。而右边我们看到S0->S1的跳转得分1.6被编码到状态1跳回到初始状态0的ε跳转里了,因为在左边的拓扑结构里S0后面(这里是只可以)可以是S1。
这种分解里,左边的拓扑结构更加简单,它的输入是一个符号(比如”S0,S1,S3”我们应该看成一个符号而不是符号序列),输出是phone。同一个phone的所有的状态跳转顺序和概率都编码在右边的声学匹配WFST里了。
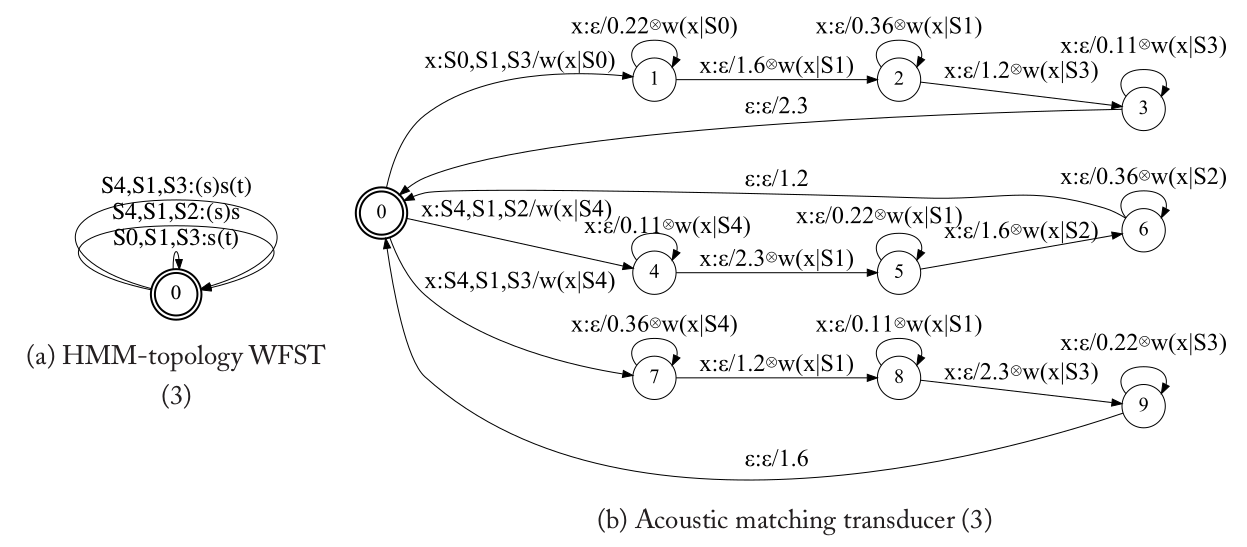
这三种分解方式的分解需要解码器在通用性(generality)和效率(efficiency)之间进行权衡。后两种的效率会更高一些,因为它们的拓扑结构WFST更加简单,而声学部分是由特定的程序实现,这些特定程序会比通用的WFST更加高效。但是第一种方式更加通用,它可以处理任何类型的HMM拓扑结构(只要拓扑结构可以用WFST来表示)。而后两种方式如果要处理新的HMM拓扑结构,在解码器的代码就要作相应的修改来适应这种特定的HMM拓扑结构。
把H分解后,拓扑结构会和C、L和G进行复合,因此我们后面的复合里的H指的是拓扑结构的H,它的输入是HMM共享状态的ID序列,输出是上下文相关的phone序列。因此$H \circ C \circ L \circ G$的输入也是共享状态的ID序列。在有的实现里,H可能是上图(a)的拓扑结构的WFST,然后链式(一个状态只能跳到另外一个状态)的跳转被合并成类似上图(a)输入,比如H、C、L和G复合后”S0,S1,S3”是一个链,为了效率更高,我们可以把它们合并成一个符号,这个过程后面会介绍到。而在另外一些实现里,H完全由程序来处理,只有$\text{CLG}=C \circ L \circ G$是提前构造和优化好的,然后由程序来实现H与CLG的复合。
上下文相关处理的FST(C)
前面我们介绍过,在大部分LVCSR系统里都是要上下文相关的phone单元来作为子词的声学建模。这些子词单元通过它们的上下文依赖在搜索网络中被连接起来。而处理这些上下文相关的phone的连接的FST就是本节要介绍的C。
如果上下文只依赖于左右各一个phone(也就是常见的triphone),则C并不难构造。任何两个phone的pair都会作为一个状态,而每个triphone都会作为一条边。边的起点状态的phone pair必须匹配triphone的左边上下文和中心的phone,而终点状态的phone pair必须匹配triphone的中心phone和右边上下文。
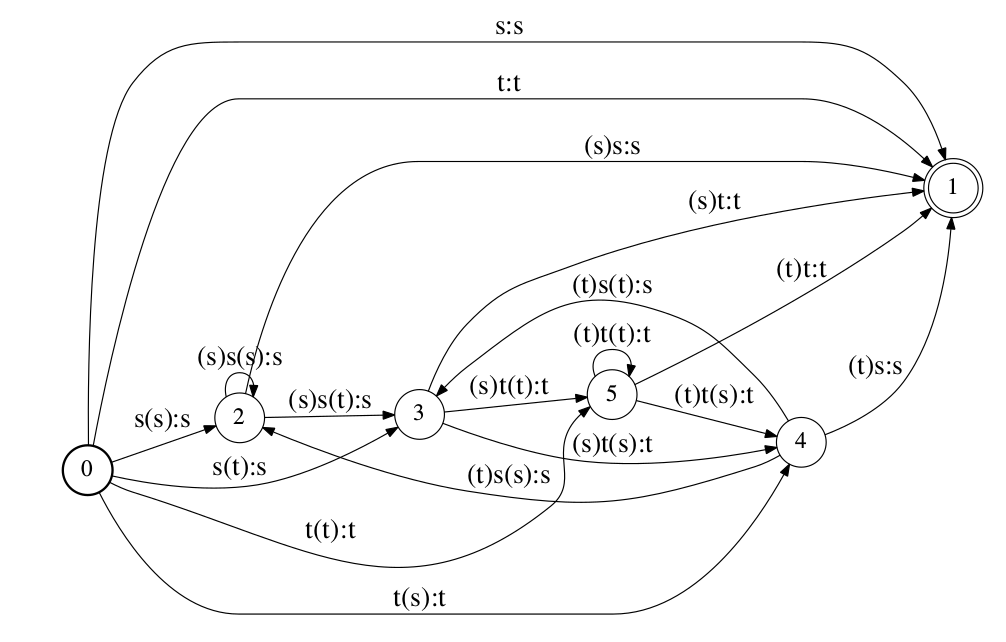
下图是一个C的简单示例,它表示只有两个基本phone /t/和/s/的请看。每个跳转的输入是triphone,输出是上下文无关的triphone的中心phone。但是这里初始状态0是没有左边上下文而终止状态1是没有右边上下文的,因此这不是跨词(cross-word)的triphone。
我们可以用一个例子来验证这个FST确实可以把一个上下文相关的triphone序列转换成上下文无关的phone序列。我们先反过来,假设要输出的phone序列是”s,s,t,s,t”,则它对应的triphone序列为”s(s)、(s)s(t)、(s)t(s)、(t)s(t)、(s)t”。下面我们来验证这个FST确实可以把triphone序列转换成phone序列。
完成这个转换的状态序列为”0->2->3->4->3->1”,请读者验证这条路径确实把上面的triphone序列变成里phone序列。
读者可能会问这个C是怎么构造出来的呢?本文没有介绍,感兴趣的读者可以参考Speech Recognition with Weighted Finite State Transducers和Investigations on Search Methods for Speech Recognition using Weighted Finite-State Transducers。
发音词典(L)
WFST L,代表发音词典,可以使用每一个词的转换机通过并与Kleene闭包运算来构造。其中每一个词的WFST是这样的:对于每一个词,根据发音词典输入是一个(或者多个)子词单元的phone的序列,而输出是这个词。对于连续语音识别来说,一个词之后可以跟任何其它词(也包括它自己,如果想约束语法,可以在后面的G里面来约束),所以L是每一个词的WFST的并与Kleene闭包。
下表是发音词典的一个简单示例,左边是词,右边是它们的发音。虽然这里的示例每个词只有一种发音,但是实际的系统一个词可以有多个发音,并且每个发音有不同的概率。
| 词 | 发音 |
|---|---|
| <s> | SIL |
| </s> | SIL |
| START | s t aa r t |
| STOP | s t aa p |
| IT | ih t |
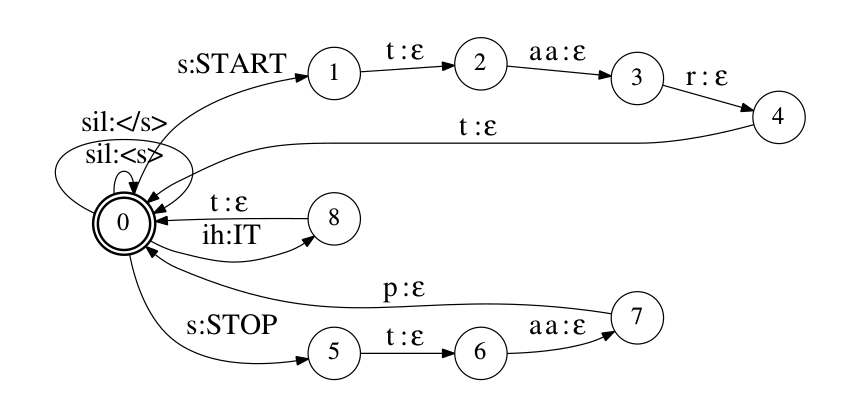
下图是代表上表的发音词典的WFST,每一个词都是从状态0开始然后结束与状态0的环。通过这个WFST,phone序列”s t aa p ih t”可以被转换成词序列”STOP IT”,对应的状态序列是0->5->6->7->0->8->0。因为这里一个词只有一个发音,所以这里假设词w的发音概率$P(v \vert w)$总是1。所以在图中我们省略了这个概率。但是如果一个词有多个发音,那么概率可能不是1,这个概率一般可以放在从初始状态0出发的那条边上。
除了表格之外,还有一种更加灵活的方式来描述发音词典,那就是使用正则表达式来描述一个词的多个发音。因为正则表达式可以转换成一个有穷自动机,所以我们可以首先用一个自动机来表示每一个词的一个或者多个发音,每个自动机的输出是词,然后我们使用并以及Kleene闭包运算来构造L。本文我们不会介绍使用正则表达式来构造自动机的方法,感兴趣的读者可以参考Introduction to Automata Theory, Languages, and Computation (3rd Edition)的第3章。
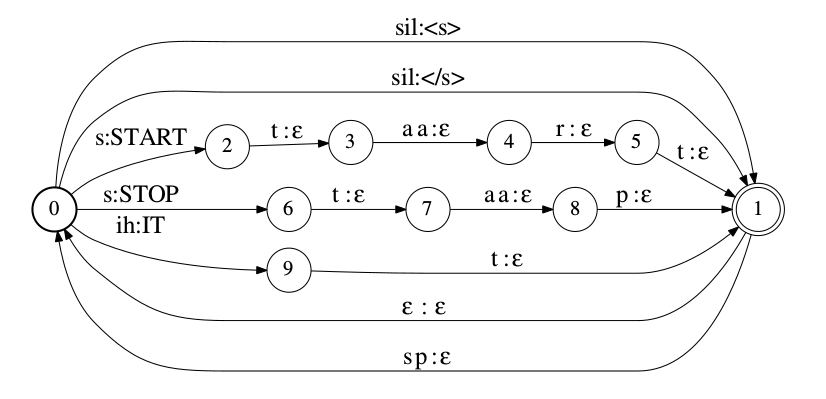
此外,我们稍微讨论一下怎么在任何两个词之间插入一个短暂停(short pause)的方法。如果语言模型有一个特殊的短暂停的”词”,那么我们只需要在发音词典里把它当成普通的词来处理就行。但是一般语言模型都不会有这样一个特殊的词,所以在发音词典的WFST里需要特殊处理短暂停。一种简单的方法是在初始状态插入一个自跳转,自跳转的边为”sp:ε”。这里的”sp”是短暂停的意思,它是声学模型的一个phone(它表示没有人在说话)。通过这种方法,两个词之间可以插入0个或者任意多个短暂停。我们也可以给这个跳转上较小的weight,从而让模型尽量不要插入过多短暂停。如果我们不想让短暂停重复(多于1次就不是”短”的暂停了?),那么可以构造L是进行特殊的处理。比如下图就是一种处理方式。通过引入一个特殊的结束节点,然后在结束节点到开始节点间加入”ε:ε”和”sp:ε”两边,就可以在每个词结束后出现0个或者1个短暂停,但是不能连续出现多个短暂停。但是这种方法会让最终复合后的WFST变大。更多节省内存的处理短暂停的方法可以参考Silence models in weighted finite-state transducers。此外,处理非语音(non-speech)事件以及短暂停的技巧也可以参考Silence is golden: modeling non-speech events in WFST-based dynamic network decoders。
语言模型(G)
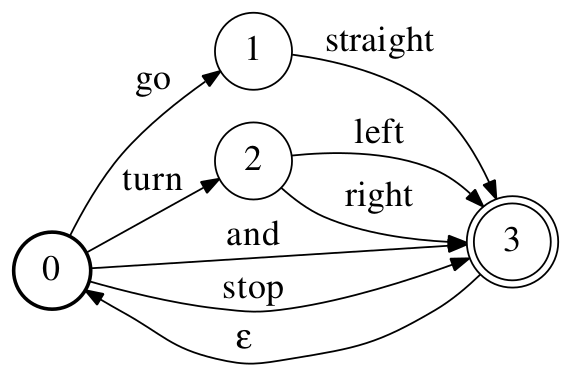
如前面介绍过的,有限状态文法(FSG)和n-gram模型是在语音识别里被广泛使用的语言模型。因为FSG是有限状态模型,任何FSG或者概率的FSG都可以很容易的转换成FSA或者WFSA。不过和前面介绍的FSG不同,在FSA里词的输入符号需要放到跳转上而不是像FSG那样放在状态上。下图是与前面介绍的FSG等价的FSA,它把FSG的词的输入符号从状态移到了跳转上。
n-gram模型等价于(n-1)-阶的马尔科夫模型,因此可以表示为WFSA。对于(n-1)-阶的马尔科夫模型来说,需要有$\vert V \vert ^{n-1}$个状态以及$\vert V \vert ^n$个跳转,这里$\vert V \vert$表示词典的大小。每一个状态表示(n-1)个词的历史(history),每一个跳转表示在这个历史的条件下出现下一个词的概率,这个概率作为WFSA的weight放在边上。
但是$\vert V \vert$通常很大,比如标准的LVCSR系统里$\vert V \vert \le 50$,当n=3的时候WFSA的状态数量就非常庞大了。比如它需要$50,000^2$个状态和$50,000^3$条边。因此,当增加$\vert V \vert$或者n时,WFSA需要的内存会急剧的增大。这个问题可以通过back-off来把训练数据中没有出现过的n-gram(只有back-off的概率)去掉,从而可以缓解内存过大的问题。前面介绍过,back-off平滑是一种用m-gram的概率来估计训练数据中没有出现过的n-gram的概率的一种方法。通过这种方法,我们的WFSA只需要记录观察到的n-gram。而未见过的n-gram通过back-off系数和其m-gram来计算,这样可以极大的减少WFSA的大小。
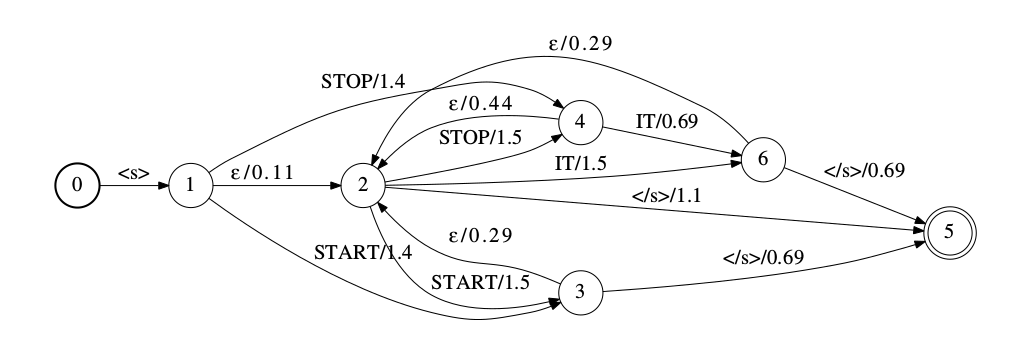
上图是表示一个back-off bigram模型的WFSA。对于一个bigram模型,每一个状态表示一个词的历史,除此之外还有一个特殊的状态表示没有历史的回退状态。在上图中,状态2是这个特殊状态。除了初始状态0、回退状态2和终止状态5,其他的每一个状态都对应一个词的历史。在这里状态1、3、4和6分别对应词”<s>”、”START”、”STOP”和”IT”。”<s>”和”</s>”是特殊的符号,分别表示句子的开始和结束。在这个示例WFSA里,bigram概率P(IT|STOP)是0.5,这个概率会作为状态4到6的跳转的weight——$-logP(\text{IT} \vert \text{STOP})=-0.69$(假设是热带半环)。
如果一个bigram $w_1w_2$在训练数据中没有出现过,也就是$C(w_1, w_2)=0$,则它的概率为$P(w_2 \vert w_1)=\alpha(w_1)P(w_2)$。假设我们需要用上图的WFSA来计算bigram P(IT|START)。首先我们考拉从状态3(START)到状态6(IT)的跳转。但是它们之间并没有直接的跳转,原因是训练数据中没有出现过”START IT”。因此,我们首先需要从状态3通过ε跳转回退到状态2,回退的weight为$-log \alpha(\text{START})=0.29$。然后unigram的概率的weight$-logP(\text{IT})=1.5$被累加进去,这是状态2到状态6的边上的weight。因此bigram的weight $-logP(\text{IT} \vert \text{START})$可以通过回退机制从路径3->2->6来计算。对于词序列”<s> START IT STOP IT </s>”,我们可以通过路径0->1->3->2->6->2->4->6->5上的边的weight的累加来计算其概率。
对于高阶的n-gram模型,回退机制和bigram类似,每一个状态代表一个长度为m个词的历史,其中$0 \le m < n$。如果我们在当前状态找不到去某个词的跳转,则我们可以通过回退的ε跳转来把历史减少为m-1个词。这个回退的过程可以一种递归下去直到找到里更短的m-gram或者当m变成0(unigram)。注意WFSA里的回退机制的实现和之前语言模型的介绍稍晚有些不同,因为在解码的时候语言模型的WFSA是需要和其他的WFST进行复合。对于用WFST实现的Viterbi算法,我们是寻找把给定输入序列的前提下(输出序列可以是任何序列)weight最小的路径。事实上,通过回退,一个输入序列可能对于多条成功的路径。比如计算概率P(IT | STOP),我们可以走路径状态4->6,也可以走另外一条回退的路径4->2->6。如果$P(\text{IT} \vert \text{STOP}) \le \alpha(\text{STOP})P(\text{IT})$,则回退机制没有问题,因为weight最小的路径就是4->6。否则它计算的概率就不正确。因此上面的回退方法只能认为是n-gram的WFSA的一种近似方法。近似的正确性依赖于回退平滑的打折算法,不过这通常不会有什么问题,因为回退的概率通常都会比观察到的n-gram的概率要小的多。因此在基于WFST的语音识别系统里,语言模型的这种近似的WFSA实现被广泛使用。此外在热带半环半环上存在实现精确回退机制的方法,但是它需要更多的状态和跳转。由于近似的语言模型WFSA和精确的WFSA的最终识别效果差别微乎其微,所以一般大家都使用这种近似方法。
下面是从n-gram语言模型构造WFSA的算法。这个算法用于在热带半环上构造回退机制的近似WFSA。在这个算法里,我们用历史(h)来表示一个状态,这里的h可以是一个词序列、一个词或者空的历史(用ε表示)。我们用特殊的符号”-“来表示WFSA的初始状态。
在第1和第2行,处理初始状态(-)和句子开始状态(<s>),它们对应上图的状态0和1。第3行在状态(-)和(<s>)之间建立一条边,它的weight是$\bar{1}$。
第4行,状态(<s>)被push到队列S里,然后第5-36行的while循环是构造WFSA的主要代码。注意这个算法可以是任何的队列。第6和7行从队列里取出一个状态,它是m个词序列的历史,$v_1^m$。第8-12行,如果历史$v_1^m$不是空,则增加一条回退的跳转,回退到状态$v_2^m$,当然需要考虑这个状态还不存在的情况,需要把它加到状态集合Q里。增加的跳转为${((v_1^m), \epsilon, −log \alpha(v_1^m), (v_2^m ))}$。如果$m<k$,则我们认为$v_k^m$是空字符ε。回退跳转的概率是$\alpha(v_1^m)$,因为这里假设是热带半环,所以这条边上的weight是$-log \alpha(v_1^m)$。
第15-35行,对于训练数据里出现在$v_1^m$后的每一个词w,我们构造一个新的状态(当然可能已经存在了)和一个新的跳转,其weight对于概率$P(w \vert v_1^m)$。第16-22行处理特殊的句子结束</s>。状态(</s>)是WFSA的结束状态,如果一个状态$v_1^m$进入结束状态后就不会有后续的输入了,所以任何状态在遇到</s>后进入这个介绍状态。
如果w不是句子结束,则需要从状态$v_1^m$创建一条边,第24-32行就是准备这条边的终点。如果m小于n-1,则终点状态s是$v_1^m$在加上w,如果m等于n-1了,则需要截取历史的第一词,用$v_2^m$加上w得到s(否则历史的词的个数就超过n-1了)。这样就可以保证状态(词序列)的长度不会超过n-1。在第33行会增加一个新的跳转到集合E,其中起点是$v_1^m$,终点是s,输入符号是w,weight是$-log P(w\vert v_1^m)$。在这之前的第29-32行,如果状态s不在Q里,需要把它加到Q里,并且加到队列S里。当队列S为空时,所有跳转的起点都处理完了,因此整个模型都处理完了。
实际训练数据里观察到的n-gram的数量会远远小于$\vert V \vert ^n$,但是当$\vert V \vert$和n增加时n-gram的数量还是会增加的比较快。原则上来说,我们可以裁剪掉对于最终语音识别准确率影响很小的n-gram,这些被裁剪的n-gram的概率会用回退概率来替代。通常我们可以去掉低频的n-gram或者基于熵的裁剪技巧。通过这些技巧,我们可以减小n-gram WFSA的大小从而使得解码速度更快,因为$H \circ C \circ L \circ G$里最大的就是语言模型G。
在构造完表示语言模型的FSA或者WFSA之后,因为我们需要把它和发音词典L进行复合,所以要把它转换成等价的WFST。这个转换也非常简单,我们只需要让WFST的输入和输出符号完全相同就可以了,其他的状态和跳转完全一样。比如上图的WFSA里状态1到3的边是”START/1.4”,我们可以转换成”START:START/1.4”。
复合与优化
在复合运算之前,我们需要修改H、C和L以便在后续的优化过程中可以确定化(determinizable)。我们把修改后的这些WFST记作$\tilde{H}$、$\tilde{C}$和\tilde{L}。这里G我们一般可以认为是可以确定化的。对于使用回退的n-gram的WFST,虽然有ε跳转,但是如果我们把ε当成普通的符号,它也是可以确定化的。在确定化的运算里,我们通常假设ε是一个普通的符号。
这样,我们的复合与优化过程为:
\[N = fact(\pi_\epsilon(min(det(\tilde{H} \circ \tilde{C} \circ det(\tilde{L} \circ G)))))\]其中det(·)和min(·)代表确定化和最小化运算。fact(·)和$\pi_\epsilon(·)$代表分解(factorization)和辅助符号消除(auxiliary symbol removal),这两个运算后面我们会介绍。最终,通过上面的公式我们得到里用于解码的WFST N。这个WFST构造好了之后,只要H、C、L和G不发生变化,我们就不需要重新构造N,每次解码时都是重复使用这个N。
首先我们来修改发音词典L。这里我们最关注的是它是否可以确定化。L通常是不能确定化的,原因(之一)是同音词的存在。在这种情况下,L不是functional,也就是说一个phone的序列可以转换成多个词序列(或者说存在多个词序列的phone序列相同)。functional是一个转换机可以确定化的充分条件。为了让L可以确定化,我们会插入辅助(auxiliary)符号来区分发音相同的词,从而使得L是functional。因为这些辅助符号只是为了复合后的N是确定化的,所以在最终确定化完成后它们会被替换成ε。为什么要替换成ε呢?因为这些辅助符号并没有真的对于输入的语音,所以需要替换成ε。
对于WFSTL,在一个词对应的phone序列的最后增加一个辅助符号等价于如下的方式修改发音词典:
night n ay t #1
knight n ay t #2
这里同音词”night”和”knight”通过辅助符号#1和#2可以彼此区分开来(当然确定化完成后,把辅助符号变成ε后它们又不可区分了,这显然的必须的,因为如果输入的phone序列是n ay t,你就应该识别出这两个词来!)。如果发音词典最多的同义词的个数是M(或者更精确的说同义词组成的集合元素最多的那个),则我们需要#1、#2,…,#M个辅助符号。
即使给定一个发音只有一个词,也就是说不存在两个发音相同的词,我们也最好插入一个辅助符号,原因是虽然任意两个词的发音不同,但是两个词序列(多个词)的发音可能相同。比如”tonight”和”to night”这两个词序列的发音序列是相同的,都是”t ax n ay t”。因此L不是functional。为了确保他是functional的,我们对于非同音的词也加一个#1。这样”tonight”和”to night”的发音序列是不同的,分别是:”t ax n ay t #1”和”t ax #1 n ay t #1”。我们把包含辅助符号的发音词典WFST记作$\tilde{L}$。
接下来我们把$\tilde{L}$和G复合,然后在确定化:
\[LG=det(\tilde{L} \circ G)\]如果G是前面介绍的back-off的n-gram对应的WFST,则我们在复合是需要使用2-状态的(epsilon-sequencing)的filter(忘了的读者可以复习一下WFST的复合运算),这样复合后的WFST会保持G中ε跳转的个数。
严格来讲,G不是确定化的WFSA,因为回退ε跳转的存在,给定一个词序列存在多条路径与之对应。但是如果我们把输入的ε当成普通的符号,则这个WFSA是(已经)确定化的。回退的路径可以通过ε的数量来区分彼此,ε的数量就是路径中回退跳转的数量。因此,为了确定化$\tilde{L} \circ G$,在复合之前这些ε都不能被去掉,否则即使$\tilde{L}$中的发音是可以区分的,我们也不能保证$\tilde{L} \circ G$是可以确定化的。因为3-状态(epsilon-matching)filter同时消费掉G的输出ε和$\tilde{L}$的输入ε,G中原有的ε数量不会被保存。因此3-状态的filter复合后我们不能区分这些回退路径。而2-状态的filter在符号后的$\tilde{L} \circ G$里是保留了ε的。
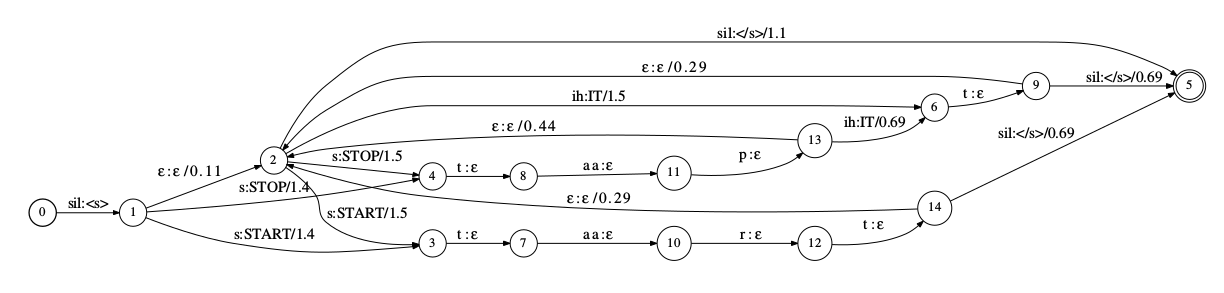
下面两个图分别是$L \circ G$和$det(L \circ G)$的例子,这里为了简单,我们没有加入辅助符号。我们看到$det(L \circ G)$比$L \circ G$小得多(其实这个简单的例子并不明显),并且它的每个状态在给定一个输入符号时最多只有一个跳转,因此它是确定化的WFST。
我们来看句子”<s> STOP IT </s>”的识别过程,它对应的输入序列是”sil s t aa p ih t sil”。对于没有确定化的$L \circ G$来说,在输入sil进入状态1,接下来的输入s会同时进入状态4和3,因此这是不确定的WFST。而对于$det(L \circ G)$,识别”sil s t aa p ih t sil”存在唯一的状态序列”0->1->3->6->8->10->5->7->4”。注意:这里要把ε看成一个普通符号才是确定的,否则如果ε是特殊的空字符,那么还存在路径”0->1->2->3->6->…..”。
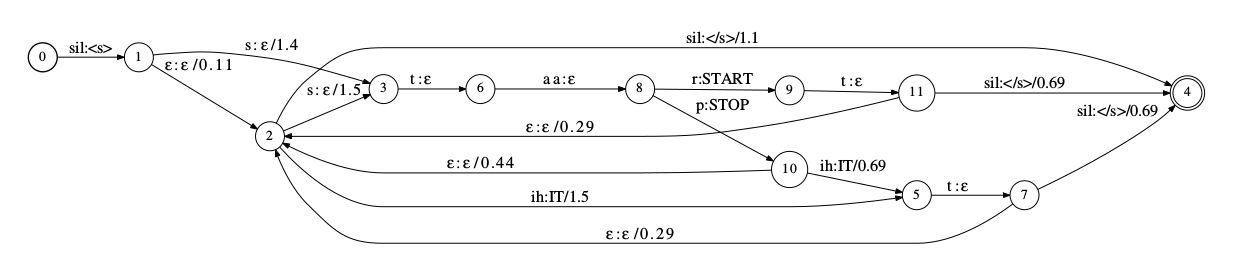
构造LG之后,我们需要把它和C进行复合。但是在复合之前让C它关于输出符号是确定化的会非常重要,所谓关于输出符号是确定化的意思是在任何状态,不存在两条边的输出符号是相同的。为了得到这样的C,我们可以先对C求逆(从而输入和输出交换),然后在确定化,然后再求逆回来,也就是invert(det(invert(C))),这里的invert(·)表示WFST的求逆运算。对于上图的triphone的WFST C,下图是经过上述处理的结果。
读者可以验证一下这个WFST确实任何一个状态出发的两条边的输出符号都是不同的,而上图的状态2->3以及2->1的输出符号都是s,所以它不是关于输出符号确定化的。
因为C’关于输出符号是确定化的,所以$C’ \circ LG$的大小不会比LG大多少。因为C’的每一个状态的对于给定输出最多一条边,所以对于C’的一个输入序列对应的每一条成功路径(因为C’不是对输入确定化的,所以可能有多条成功路径)来说,而LG又是确定化的,所以一条路径最多复合出一个结果。此外,如上图所示,除了初始状态有ε跳转之外,C’对于输入符号也几乎是确定化的。因为这个原因,$C’ \circ LG$很可能已经就是确定化的WFST。所以通常对于$C’ \circ LG$的结果不在需要进行确定化运算。
此外,在与LG复合之前,我们不能忘了往C’里插入辅助符号。LG包含后续优化步骤需要的辅助符号。但是C’里并没有#1这样的输出符号,所以在复合的时候这些辅助符号会丢失掉。因此,我们需要在C’的每一个状态都增加M(M是辅助符号的个数)个自跳转,这些自跳转的输入和输出都是相同的辅助符号,这样复合是任何词的发音后面都可以插入任何辅助符号(当然有很多是不需要的,复合的时候就没有了)。比如发音词典里同音词的最大数量为M,则C’的每个状态都需要加M个自跳转,其输入和输出符号都是#1, #2, …。我们把增加里自跳转的C’记作$\tilde{C}$。这样:
\[CLG=\tilde{C} \circ LG\]得到的CLG依然包含辅助符号,这些符号使得CLG可以确定化。
接下来,我们需要修改H,对它的初始状态(而不是想C’那样每个状态)增加处理辅助符号的自跳转。如上面3个图所示,我们假设初始状态是任何phone的边界(任何一个phone的开始和结束都是初始状态),所以我们只需要在初始状态插入M个辅助符号的自跳转。我们把修改后的H记为$\tilde{H}$,这样最终复合与确定化的结果为:
\[HCLG=det(\tilde{H} \circ CLG)\]然后我们把HCLG最小化并且删除辅助符号(替换成ε),得到:
\[HCLG'=\pi_\epsilon(min(HCLG))\]上式中$\pi_\epsilon(·)$是把所有的辅助符号变成ε。
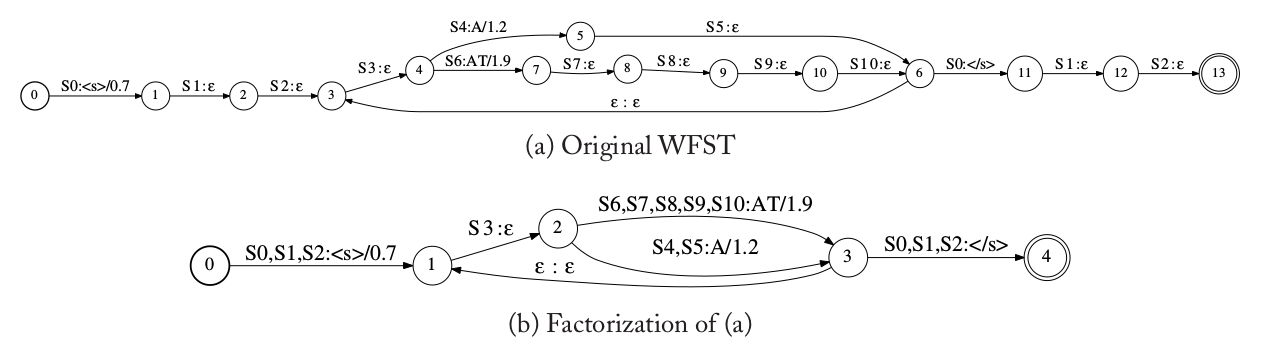
最后我们对HCLG’进行分解(factorization,这个翻译有些不合适,其实是把链式的状态序列合并,但是我找不到合适的词),得到:
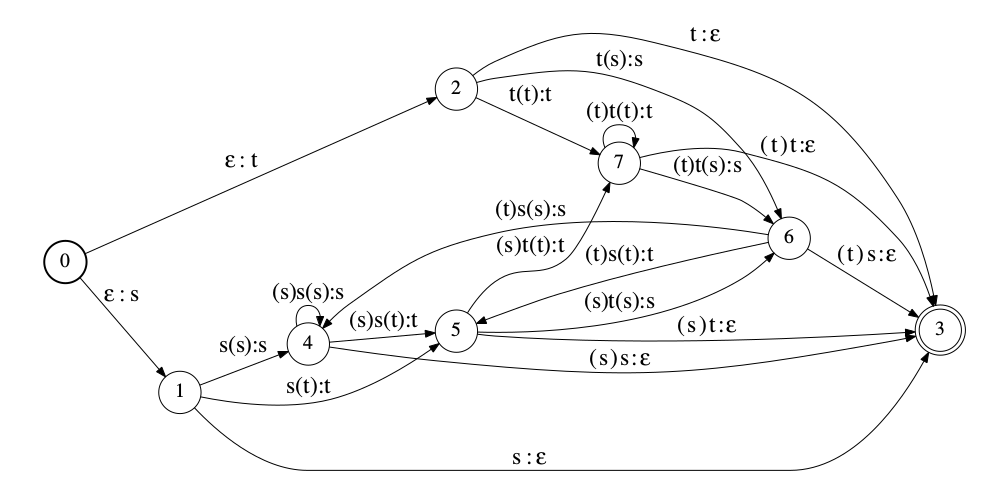
\[N=fact(HCLG')\]分解可以减少WFST的大小。通过把链式的跳转序列合并成一个跳转,我们可以减少HCLG’的状态和跳转个数。合并链式的序列后的输入/输出符号序列需要连接起来,weight需要用$\bigotimes$乘起来。下图是分解的示例,其中图(a)是原始的WFST,而图(b)是分解后的结果。
在分解后的WFST里,每个跳转的输入符号不再是一个字符(共享状态),而是一个状态的序列,并且这个状态序列类似于上图(a)的一个输入——一个子词单元的HMM,比如S0,S1,S2对应triphone s(t)。子词单元的HMM内部的跳转需要解码器用类似上图(b)的方式用代码来实现。注意:上图(b)的每个共享状态序列的程度并不相同,这和上图(a)是不一样的。
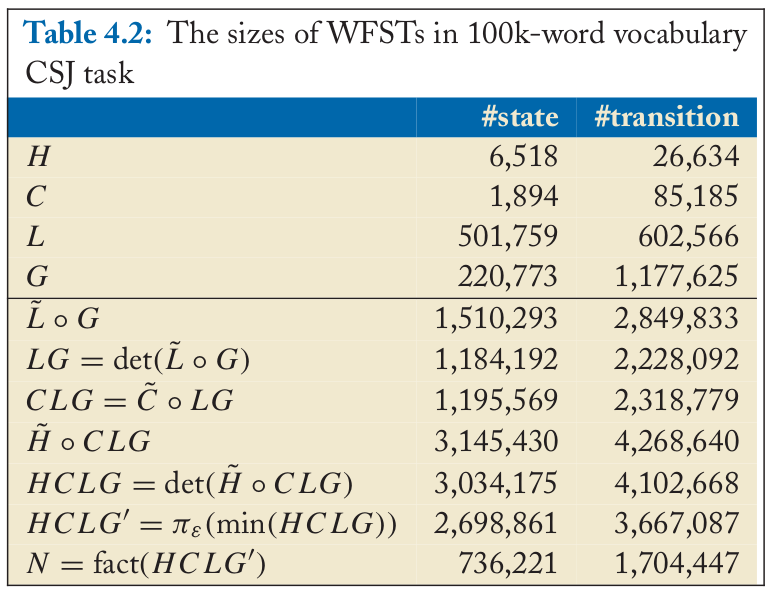
下表我们展示里通过如上步骤生成的WFST的大小。我们使用Corpus of Spontaneous Japanese (CSJ)语料库来构造发音词典、声学和语音模型。这个词典包含2,000个10到30分钟的上课的录音。声学模型有5,000个共享的状态,每一个状态都是一个高斯混合模型。发音词典包含的词汇量为100k。语言模型是这些录音的转录文本(transcript)训练的back-off trigram模型。如下表所示,复合后得到的N的大小大约是语言模型WFST G的1.5倍,因此复合后并没有显著的增大WFST的大小。
使用WFST的解码算法
本节会介绍使用一个完全复合后的WFST的解码算法,它是基于时间同步的Viterbi beam搜索算法。虽然这个算法和前面介绍的算法很类似,但是为WFST的处理做了一些扩展。下图是这个算法的主要流程的伪代码,对于输入特征向量序列X=x[1],…,x[T],它会调用初始化、处理ε跳转、处理普通跳转已经最终处理等函数。这个算法最终会使用回溯来得到最小weight的路径,从而得到语音识别的结果。
在下面的代码里,我们需要使用到如下变量,这和前面非WFST的解码算法类似。
- $\alpha(t, s)$
- 一个t时刻处于状态s的部分(partial)的路径的累计weight。对于热带半环,它是Viterbi得分的取反。
- B(t, s)
- 保存t时刻处于状态s的最佳路径的回溯指针。B(t, s)的值是一个pair $<\tau, e>$,其中$\tau$表示e的开始帧的时间,而e是t时刻进入状态s的最可能的跳转。如果e=0,则表示没有进入s的跳转。
- $\alpha(t, e, j)$
- t时刻位于跳转e的第j个HMM状态的累加weight。
- b(t, e, j)
- t时刻位于跳转e的第j个HMM状态的最佳路径的回溯指针。b(t, e, j)记录跳转e的开始帧的时间。
注意:这里有两个”状态”一定需要区分。一个是WFST的状态,一个是HMM的状态。WFST的状态就是我们前面构造的$H \circ C \circ L \circ G$的状态,它的输入符号是上图(b)“S0,S1,S2”这样的符号。S0、S1和S2是一个HMM的状态(这3个是普通状态,还有特殊的开始和结束状态用$i_e,f_e$表示),0和1是WFST的状态。从WFST的状态0跳到状态1需要经过S0->S1->S2。所以我们会说从WFST的状态0进入这条边,它的含义是进入S0,当然WFST的weight(这里为0.7)是在进入的时候处理,而在这条边里,我们可能需要消耗很多帧的输入特征,这里会涉及HMM的跳转概率和发射概率。最终会从S2跳到HMM的终止状态,从而结束这条边进入WFST的状态1。然后WFST又会从状态1进入下一条边”S3”……
在下面的伪代码里,每个跳转的输入符号可以是一个HMM状态的序列,它可以被认为是一个子词单元的HMM,但是不一定要对应到一个triphone模型。比如,上图(b)的输入符号”S0,S1,S2”、”S3”、”S4,S5”和”S6,S7,S8,S9,S10”可以被看作子词单元。我们假设这样的子词单元的HMM对应的跳转e有一个特殊的没有发射概率的初始状态$i_e$和有一个终止状态$f_e$,剩下的就是普通的有发射概率的HMM状态。我们也引入一个声学weight函数$\omega(x,k \vert \mathcal{M},j)$来表示从子词HMM模型$\mathcal{M}$的状态j跳到状态k并且发射特征向量x的weight,它的计算方法为:
\[\omega(x,k \vert \mathcal{M},j)=\begin{cases} -log a_{jk}^{\mathcal{M}} b_k^{\mathcal{M}}(x) & \text{if} x \ne \epsilon \\ -log a_{jk}^{\mathcal{M}} & \text{if} x = \epsilon \end{cases}\]初始化函数$\text{initialize}(I, \lambda)$如下所示。
上面的代码用初始状态集合I和初始weight函数$\lambda$来初始化第0帧的$\alpha(t,s)$,对于$i \in I, \alpha(0,i)=\lambda(i)$,用自然语言来描述就是在0时刻,处于初始状态i的概率为$\lambda(i)$。而回溯指针B(0,i)都设置为<0,0>。接着把所有的初始状态插入到队列S里作为当前活跃的状态。
然后主函数里的for循环会处理每一个时刻t,对于输入向量x[t],首先是处理ε跳转,然后是处理普通的非ε跳转。处理ε挑战的函数为transition_with_epsilon(E, S, t),代码如下。
上面的代码循环的处理活跃的状态集合S,直到它为空为止。第5-14行是循环的主体,它对于S里的每一个状态s,更新终点状态的weight和回溯指针。其中第5-14行是遍历状态s的所有ε跳转,第6行计算t时刻从s通过ε跳转e跳到n[e]的weight。第7行是比较这条新的路径的weight和原来的weight哪个好,对于一个幂等的半环比如热带半环来说,如果$\alpha \bigotimes \alpha’=\alpha’$,则说明$\alpha’$比$\alpha$要好,比如在热带半环里$\bigotimes$是min,$min(\alpha, \alpha’)=\alpha’$的意思就是$\alpha’ < \alpha$,因此$\alpha’$是更好的一条路径。如果新的路径更好,则更新$\alpha(t,n[e])$和B(t,n[e])。其中B(t,n[e])=<t,e>表示t时刻进入n[e]状态的最优边是e,并且进入的时刻是t(ε跳转不消耗输入符号)。第10行把没有处理过的n[e]加到S里,以便可以处理连续的ε跳转。第15-17行,如果状态s至少存在一条非ε的跳转,则把它加到S’里,后面处理普通跳转的函数会用到S’。判断s是否至少存在一条非ε跳转是第15行$\{e|e \in E(s), i[e] \ne \epsilon\} \ne \emptyset$,它首先找到从s出发的非ε跳转组成的集合,然后判断这个集合是否为空。
处理普通跳转的函数transition_with_input(E, S, A, x, t)的伪代码如下:
第1-9行,处理S中每一个活跃状态s出去的每一个跳转e的HMM状态(跳转e包含里多个HMM状态)。对于跳转e的初始状态$i_e$,累计的weight$\alpha(t-1, e, i_e)$和回溯指针$b(t-1, e, i_e)$会被计算。注意在t时刻实际处理的是t-1,因为进入初始状态是不需要消耗输入符号的。 S里是t-1时刻处于WFST状态s的集合,我们考虑s出去的每一条普通的边e,进入e的HMM初始状态$i_e$,它的weight是$\alpha(t-1, s) \bigotimes w[e]$,回溯的指针$b(t-1, e, i_e)=t-1$表示进入e的$i_e$状态的时刻为t-1。第5-7行把$<e, i_e>$对加到队列A里,队列A表示活跃的<边,HMM状态>对。
HMM内部的状态跳转是在第10-24行处理的。对于A里的pair <e,j>,我们处理t-1时刻处于j而t时刻处于k的跳转。第14行遍历状态j的所有可以跳过去的状态k,前提是k不是HMM的终止状态(终止状态在下面特殊处理)。我们计算这个跳转的得分$\alpha’ = \alpha(t-1, e, j) \bigotimes \omega(x,k \vert i[e], j)$,也就是t-1处于边e的第j个HMM状态的weight乘以$\omega(x,k \vert i[e], j)$——从状态j通过符号i[e]跳到状态k并且发射x的得分。注意这个i[e]就是前面我们介绍的子词的HMM,比如”S0,S1,S2”,则$\omega(x,2 \vert i[e], 1)$表示从S1跳到S2的概率乘以S2下发射x的概率得分。如果这个得分$\alpha’$比$\alpha(t, e ,k)$好,则更新$\alpha(t, e ,k)$以及回溯指针b(t, e, k)。第20行把新的活跃状态对<e,k>加到新的活跃HMM状态队列A’里。
第25-34行处理活跃HMM状态队列A’里的能跳到e的终止状态的那些状态k,因为跳到终止状态也不需要消耗输入(时间),所以放到这里处理。它的处理方式和前面处理非终止状态类似,只是把$\omega(x,k \vert i[e], j)$替换成了$\omega(\epsilon,f_e \vert i[e], k)$,表示没有发射概率。另外HMM的终止状态更新的是WFST的状态的$\alpha(t,s)$和B(t,s),如果读者不清楚可以回去阅读注意部分。
最终在第35行,t时刻活跃的HMM状态和WFST状态被返回,用于主函数的后续处理。
每处理完一个时刻,需要调用函数prune(S, A, t)进行裁剪,去掉不大有希望的活跃状态,代码和之前的非WFST的解码器基本类似。
第一行寻找当前活跃状态里最优的得分$w_t^{best}$,需要在S和A里寻找。然后根据$\alpha(t,s)$把得分低于阈值$\gamma w_t^{best}$的活跃状态s剪裁掉,最后根据$\alpha(t, e, j)$把得分低于阈值的<e,j>也裁剪掉。
处理完T帧的ε跳转和普通跳转之后,我们需要处理最后的ε跳转,算法如下:
在第3-14行,我们对T时刻在S中的活跃状态通过ε跳转进行处理。对于所以活跃的终止状态,我们找出累计weight最好的$\hat{\alpha}$以及对应的回溯指针$\hat{B}$。
找到里最好的回溯指针$\hat{B}$之后,我们可以使用下面的回溯算法找到最优的路径,代码如下:
使用WFST的Viterbi搜索算法和传统的解码算法其实很类似。和传统的方法类似,基于WFST的算法也可以扩展记录多个回溯指针来生成lattice。
解码器的性能
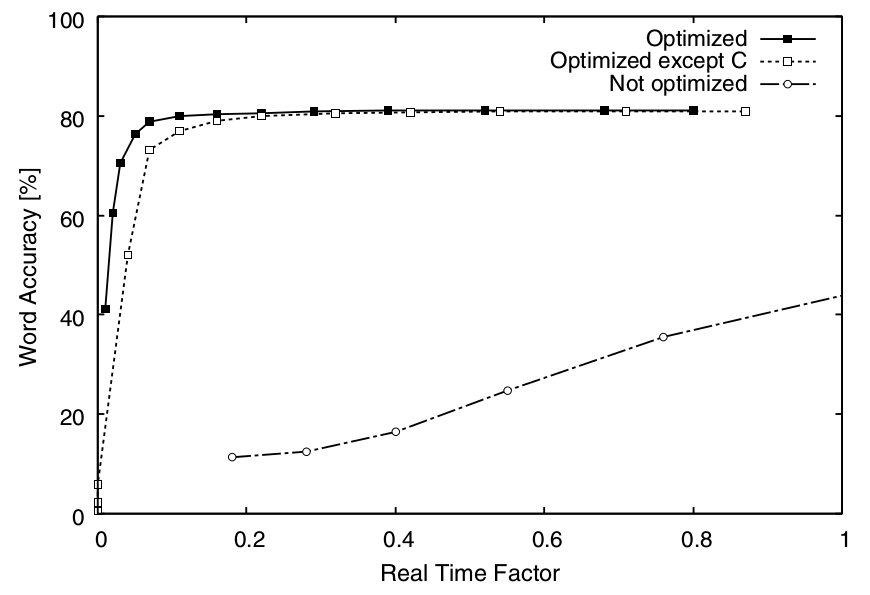
最后我们来讨论一下基于WFST的语音识别系统的解码性能。解码器的性能是通过解码的时间和识别的准确率两个指标同时来评估的,如果解码器在很短的时间内得到高准确率,则它就是一个好的解码器。对于Viterbi beam搜索算法来说,解码的时间和准确率依赖于beam的宽度(width)。如果beam的宽度较小,则解码速度会变块但是识别准确率会下降。如果我们使用很大的beam宽度,那么它的准确率会接近不使用beam剪枝的值。本节我们看一下在CSJ任务上WFST的优化对于解码性能的影响。
下图比较里不同的WFST的词准确率(word accurary)和实时率(real time factor)的关系。词准确率(等于1减去词错误率)用于衡量语音识别的准确率,它的计算公式为:
\[WACC[%]=\frac{NW − SUB − INS − DEL}{NW} \times 100\]其中NW是实际说话人说话的词的个数,SUB、INS和DEL代表替换错误、插入错误和删除错误的个数。这些错误数量可以对正确的词序列(reference)和识别的词序列(hypothesis)使用动态规划算法(编辑距离算法)来计算。实时率等于识别一段语音的时间除以说这段语音话的时间。
上图的实验里,每一条线都表示通过改变beam宽度得到准确率和实时率,线越靠近左上角越好。上图的黑色方框的线是完全优化的WFST,也就是$N = fact(\pi_\epsilon(min(det(\tilde{H} \circ \tilde{C} \circ det(\tilde{L} \circ G)))))$。白色方框的线的WFST和完全优化的基本一样,唯一的区别就是C没有对输出符号进行确定化。而圆圈的线对于的WFST完全没有优化,它等于$H \circ C \circ L \circ G$。上面的实验是使用多核的Xeon X5570 3GHz的处理器,解码器是一个进程(多线程)。结果表明WFST的优化对于解码器的性能非常重要。此外,对于C进行输出符号的确定化也很有用。此外,我们检查里在WFST的优化时应该用哪个半环。这个选择可能会影响Viterbi beam搜索的性能。事实上,不同的半环会导致在确定化或者weight pushing算法时每条路径的weight的分布不同。
在确定化算法里,当绑定(binding)状态和跳转时,weight会被push向成功的跳转。这是算法11的第9行的$\bigotimes$-求和导致的。如果我们按照前面介绍的方法来构造WFST,则N中的weight会因为确定化而得到很好的分布。在确定化$(\tilde{L} \circ G)$之前,大部分weight都分布在词内跳转的开始状态。这些weight在确定化的过程中逐渐被push到成功的跳转里。
对于weight pushing算法,weight被push到初始状态。当使用热带半环时,weight会尽可能的分布在路径的开始。而对于log半环,weight会分布的更加均匀。在Viterbi beam搜索算法的较早的时刻根据weight来剪枝掉不太可能的路径会让搜索更加快,但是会增加剪裁错误的可能性。具体选择哪个半环依赖于不同的任务。
此外,我们检查了在WFST最小化之前是否需要进行weight pushing。如果在对HCLG进行最小化之前进行weight pushin,则weight会被push到第一个词上。而确定化的weight只是在词内进行重新分配,原因是辅助符号导致的。最近的研究显示在最小化之前对log半环进行确定化并且去掉weight pushing会让解码更加高效。
下图对比了在CSJ任务里使用热带半环/log半环以及进行/不进行weigh pushing的解码器效果。这个实验显示对于WFST的优化而言,log半环比热带半环更好。此外,使用weight pusing并没有必要。注意:这只是这个任务上的实验结果,这个结论对于其他任务或者其他的优化方式并不一定成立。
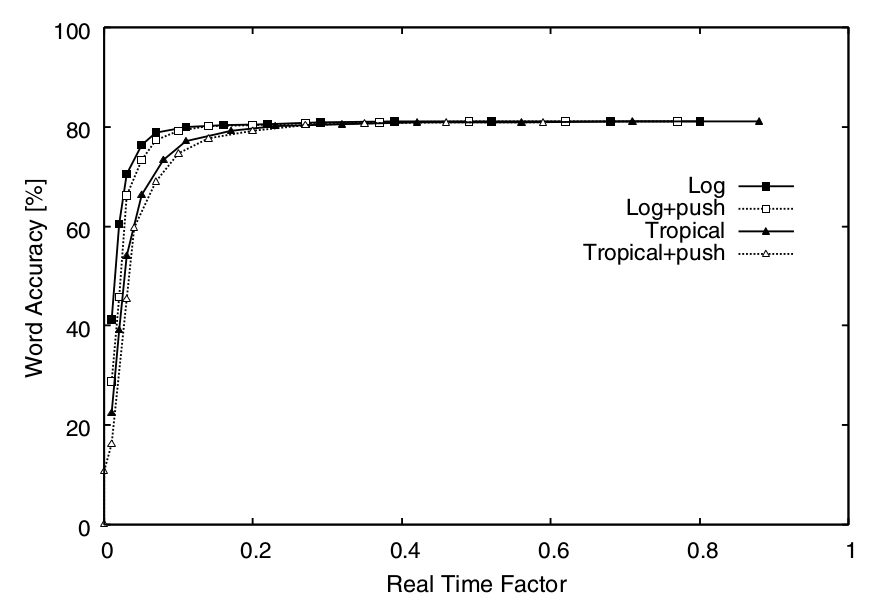 热带半环/log半环以及是否进行weight pushing的解码性能比较
热带半环/log半环以及是否进行weight pushing的解码性能比较
- 显示Disqus评论(需要科学上网)